
����Ŀ����ͼ,�ڡ�ABC��.AC=BC=5.AB=6.CD��AB������.��P�ӵ�C��������ÿ��2.5����λ���ȵ��ٶ���C-D-C�˶�.�ڵ�P������ͬʱ����QҲ�ӵ�C��������ÿ��2����λ���ȵ��ٶ��ر�CA���A�˶�.��һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�����P�˶���ʱ��Ϊt��.
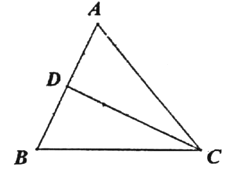
��1���ú�t�Ĵ���ʽ��ʾCP��CQ�ij���.
��2���ú�t�Ĵ���ʽ��ʾ��CPQ�����.
��3������CPQ���CAD����ʱ��ֱ��д��t��ȡֵ��Χ.
���𰸡���1����0��t��![]() ʱ��CP=2.5t��CQ=2t����
ʱ��CP=2.5t��CQ=2t����![]() ʱ��CP=8-2.5t��CQ=2t��
ʱ��CP=8-2.5t��CQ=2t��
��2����0��t��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ��2.5t��
��2.5t��![]() ��2t=
��2t=![]() ����
����![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ����8-2.5t����
����8-2.5t����![]() ��2t=
��2t=![]() .
.
��3��0��t��![]() ��
��![]() s
s
��������
��1�����������Σ���0��t��![]() ʱ����
ʱ����![]() ��t
��t![]() ʱ���ֱ���⼴�ɣ�
ʱ���ֱ���⼴�ɣ�
��2�����������Σ���0��t��![]() ʱ����
ʱ����![]() ��t��
��t��![]() ʱ������S��CPQ=
ʱ������S��CPQ=![]() PCsin��ACDCQ�ֱ���⼴�ɣ�
PCsin��ACDCQ�ֱ���⼴�ɣ�
��3�����������Σ���0��t��![]() ������֤����QCP�ס�DCA����
������֤����QCP�ס�DCA����![]() ��t
��t![]() ����QPC=90��ʱ����QPC�ס�ADC������������⼴�ɣ�
����QPC=90��ʱ����QPC�ס�ADC������������⼴�ɣ�
�⣺��1����CA=CB��AD=BD=3��
��CD��AB��
���ADC=90����
��CD=![]() =
=![]() =4��
=4��
��0��t��![]() ʱ��CP=2.5t��CQ=2t��
ʱ��CP=2.5t��CQ=2t��
��![]() ʱ��CP=8-2.5t��CQ=2t��
ʱ��CP=8-2.5t��CQ=2t��
��2����sin��ACD=![]() =
=![]() ��
��
�൱0��t��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ��2.5t��
��2.5t��![]() ��2t=
��2t=![]()
��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ����8-2.5t����
����8-2.5t����![]() ��2t=
��2t=![]() .
.
��3���ٵ�0��t��![]() ʱ��
ʱ��
��CP=2.5t��CQ=2t��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��![]() ��
��
�ߡ�PCQ=��ACD��
��0��t��![]() ʱ����QCP�ס�DCA��
ʱ����QCP�ס�DCA��
�ڵ�![]() ʱ������QPC=90��ʱ����QPC�ס�ADC��
ʱ������QPC=90��ʱ����QPC�ס�ADC��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��������������������t��ֵΪ��0��t��![]() ��
��![]() sʱ����QCP�ס�DCA��
sʱ����QCP�ס�DCA��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����B��6��0����ֱ��AB��ֱ��OA�ཻ�ڵ�A��4��2��������M���߶�OA������AC���˶���
��1����ֱ��AB�Ľ���ʽ��
��2������OAC�������
��3���Ƿ���ڵ�M��ʹ��OMC���������OAC�������![]() �������������ʱ��M�����ꣻ�������ڣ�˵�����ɣ�
�������������ʱ��M�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��ֱ������ϵ��������A����1��0����B��4��0����������y=ax2+bx��2��a��0������A��B������ΪC����P��m��n����n��0��Ϊ��������һ�㣮
��1���������ߵĽ���ʽ�Ͷ���C�����ꣻ
��2������APBΪ�۽�ʱ����m��ȡֵ��Χ��
��3����m��![]() ������APBΪֱ��ʱ���������������������ƽ��t��0��t��
������APBΪֱ��ʱ���������������������ƽ��t��0��t��![]() ������λ����C��Pƽ�ƺ��Ӧ�ĵ�ֱ��ΪC�䡢P�����Ƿ����t��ʹ����λ��������A��B��P�䡢C�������ɵĶ���ε��ܳ���̣������ڣ���t��ֵ��˵��������ƽ�Ƶķ����������ڣ���˵�����ɣ�
������λ����C��Pƽ�ƺ��Ӧ�ĵ�ֱ��ΪC�䡢P�����Ƿ����t��ʹ����λ��������A��B��P�䡢C�������ɵĶ���ε��ܳ���̣������ڣ���t��ֵ��˵��������ƽ�Ƶķ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ɫ��������������������±���
��ȡ�IJ�ɫ��������n | 500 | 1000 | 1500 | 2000 | 2500 |
�ŵ�ƷƵ��m | 471 | 946 | 1426 | 1898 | 2370 |
�ŵ�ƷƵ�� | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
��1������ͼ�����������ɫ���������ŵ�Ʒ��Ƶ�ʵ�����ͳ��ͼ
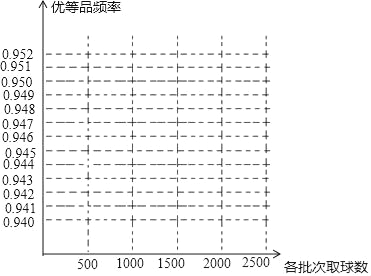
��2��������ɫ���������ŵ�Ʒ�����ʵĹ���ֵ��Լ�Ƕ��٣�����ȷ��0.01��
��3����������ɫ��������ѡ��5������13������22���������dz�����ɫ�ⶼ��ͬ�������Ƿ���һ�������Ĵ����У���Ӵ���������һ�����ǻ���ĸ��ʣ�
��4���ִӵڣ�3������˵�Ĵ�����ȡ�����ɸ�����������ͬ�����Ļ�������ȣ�ʹ�Ӵ���������һ������ĸ���Ϊ![]() ����ȡ���˶��ٸ�����
����ȡ���˶��ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼl�����ı���ABCD��.��DAB���Խ���ACƽ�֣���AC2=AB��AD�����dzƸ��ı���Ϊ���ɷ��ı��Ρ���DAB��Ϊ���ɷֽǡ�.

��1����ͼ2���ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ�����֤����DAC�ס�CAB.
��2����ͼ2���ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ��������DCB=��DAB ���DAB = .
��3�������ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ�����AC=4.BC=2.��D=90�㣬��AD= .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l������O��Բ��O��������O����A��B���㣬��C����O�ϣ�����AOC��30������P��ֱ��l�ϵ�һ������(��Բ��O���غ�)��ֱ��CP����O�ཻ����һ��Q�����QP��QO������OCP�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC��λ����ͼ��ʾ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���
��1������ABC��x�᷽������ƽ��6����λ������ƽ�ƺ�õ��ġ�A1B1C1��
��2������ABC���ŵ�A˳ʱ����ת90�㣬������ת��õ��ġ�AB2C2����ֱ��д����B2��C2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��ʾ������ a ������������� a ��ʾ���� a ����С����.���磺2.5 2 ��3 3 �� 2.5 3 ��<2.5> 3 ��<4> 5 ��< 1.5> 1 .����������⣺
��1�� 4.5 ,< 3.5> .
��2����x 2 ���� < x> ��ȡֵ��Χ�� ����< y > 1���� y ��ȡֵ��Χ�� .
��3����֪ x, y ���㷽����![]() ���� x, y ��ȡֵ��Χ.
���� x, y ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() Ϊ�����ϵ������㣬��
Ϊ�����ϵ������㣬��![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() .
.

��1������һֻ��������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ������˶���ͬʱ��һֻ��������
����λ���ȵ��ٶ������˶���ͬʱ��һֻ��������![]() ǡ�ôӵ�
ǡ�ôӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ������˶�������ֻ���������������ϵĵ�
����λ���ȵ��ٶ������˶�������ֻ���������������ϵĵ�![]() �����������
�����������![]() ��ʾ������
��ʾ������
��2������������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ������˶���ͬʱ��һ��������
����λ���ȵ��ٶ������˶���ͬʱ��һ��������![]() ǡ�ôӵ�
ǡ�ôӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ������˶�������ֻ���������������ϵĵ�
����λ���ȵ��ٶ������˶�������ֻ���������������ϵĵ�![]() �����������
�����������![]() ��ʾ����.
��ʾ����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com