
 过圆心
过圆心 ,交圆
,交圆 于
于 两点,
两点, 切圆
切圆 于点
于点 ,作
,作 ,垂足为
,垂足为 ,连结
,连结 .
. 变为图2中割线
变为图2中割线 的情形,
的情形, 与圆
与圆 交于
交于 两点,
两点, 与
与 交于点
交于点 ,
, ,写出图2中相等的角(写出三组即可,直角除外);
,写出图2中相等的角(写出三组即可,直角除外); .
.

科目:初中数学 来源:不详 题型:解答题
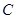 将线段
将线段 分成两部分,如果
分成两部分,如果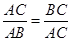 ,那么称点
,那么称点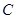 为线段
为线段 的黄金分割点.
的黄金分割点. 将一个面积为
将一个面积为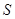 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为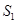 ,
,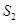 ,如果
,如果 ,那么称直线
,那么称直线 为该图形的黄金分割线.
为该图形的黄金分割线.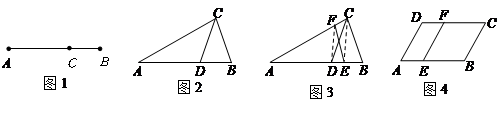
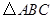 中,若点
中,若点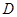 为
为 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线 是
是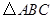 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?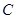 任作一条直线交
任作一条直线交 于点
于点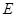 ,再过点
,再过点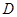 作直线
作直线 ,交
,交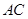 于点
于点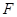 ,连接
,连接 (如图3),则直线
(如图3),则直线 也是
也是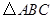 的黄金分割线.
的黄金分割线.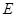 是
是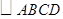 的边
的边 的黄金分割点,过点
的黄金分割点,过点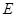 作
作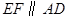 ,交
,交 于点
于点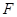 ,显然直线
,显然直线 是
是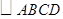 的黄金分割线.请你画一条
的黄金分割线.请你画一条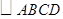 的黄金分割线,使它不经过
的黄金分割线,使它不经过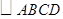 各边黄金分割点.
各边黄金分割点.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 (3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
(3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,则△A′B′C′的面积是________________.
,则△A′B′C′的面积是________________.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

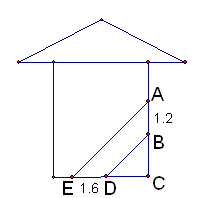
 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且 米,
米,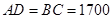 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道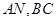 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于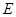 处,
处, 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.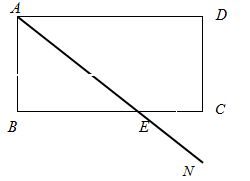
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com