
【题目】如图,已知直线y=﹣x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(1)求抛物线的解析式;
(2)观察图象,写出不等式ax2+bx+c>﹣x+3的解集为 ;
(3)若点D的坐标为(﹣1,0),在直线y=﹣x+3上有一点P,使△ABO与△ADP相似,求出点P的坐标.
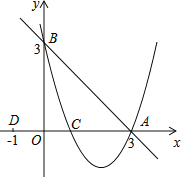
【答案】(1)y=x2﹣4x+3;(2)x<0或x>3;(3)P1(﹣1,4),P2(1,2).
【解析】
(1)根据题意首先利用交点式得出y=a(x﹣1)(x﹣3),进而得出a的值即可;
(2)由题意直接利用函数图象得出ax2+bx+c>﹣x+3的解集即为交点两侧两图象在上面的则对应函数值大,否则就小,进而得出答案;
(3)根据题意分析①若△ABO∽△AP1D,②若△ABO∽△ADP2,进而分别得出P点坐标即可.
解:(1)由题意得出:A(3,0),B(0,3),
∵抛物线y=ax2+bx+c经过A、B、C(1,0)三点,
∴设y=a(x﹣1)(x﹣3),(a≠0),
∴a×(﹣1)×(﹣3)=3,
∴抛物线解析式为:y=x2﹣4x+3;
(2)∵A(3,0),B(0,3),
∴利用图象可得出:不等式ax2+bx+c>﹣x+3的解集为:x<0或x>3;
故答案为:x<0或x>3;
(3)由题意得:△ABO为等腰直角三角形,如图所示:
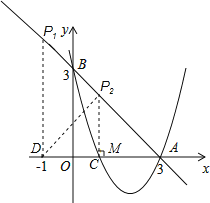
①若△ABO∽△AP1D,
则![]() =
=![]() ,
,
∴DP1=AD=4,
∴P1(﹣1,4);
②若△ABO∽△ADP2,过点P2作P2M⊥x轴于点M,AD=4,
∵△ABO为等腰直角三角形,
∴△ADP2是等腰直角三角形,由三线合一可得:DM=AM=2=P2M,
∴MO=1,
∴P2(1,2).


科目:初中数学 来源: 题型:
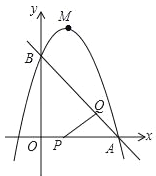
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:
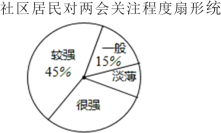
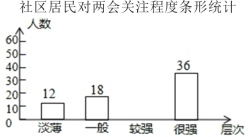
请结合图表中的信息,解答下列问题:
(1)此次调查一共随机抽取了_____名居民;
(2)请将条形统计图补充完整;
(3)扇形统计图中,“很强”所对应扇形圆心角的度数为_____;
(4)若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 _____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
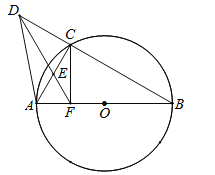
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
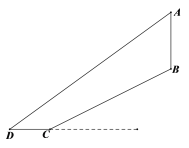
【题目】某游乐场新推出一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度,其中斜坡轨道BC的坡度为![]() ,BC=
,BC=![]() 米,CD=8米,∠D=36°,(其中A,B,C,D均在同一平面内)则垂直升降电梯AB的高度约为__________米.(精确到0.1米,参考数据:
米,CD=8米,∠D=36°,(其中A,B,C,D均在同一平面内)则垂直升降电梯AB的高度约为__________米.(精确到0.1米,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
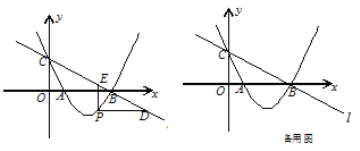
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com