
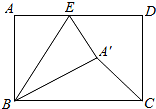
 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD 的平分线上时,CA′的长为多少?
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD 的平分线上时,CA′的长为多少? 分析 过点A′作A′M⊥BC于点M.设CM=A′M=x,则BM=7-x.在直角△A′MB中,由勾股定理得到:A′M2=A′B2-BM2=25-(7-x)2.由此求得x的值,然后在等腰Rt△A′CM中由CA′=$\sqrt{2}$A′M求解即可.
解答 解:如图所示,过点A′作A′M⊥BC于点M.
∵点A的对应点A′恰落在∠BCD的平分线上,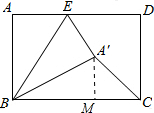
∴设CM=A′M=x,则BM=7-x,
又由折叠的性质知AB=A′B=5,
∴在直角△A′MB中,由勾股定理得到:A′M2=A′B2-BM2=25-(7-x)2,
∴25-(7-x)2=x2,
∴x=3或x=4,
∵在等腰Rt△A′CM中,CA′=$\sqrt{2}$A′M,
∴CA′=3$\sqrt{2}$或4$\sqrt{2}$.
故答案是:3$\sqrt{2}$或4$\sqrt{2}$.
点评 本题考查了矩形的性质,翻折变换(折叠问题).解题的关键是作出辅助线,构建直角三角形△A′MB和等腰直角△A′CM,利用勾股定理将所求的线段与已知线段的数量关系联系起来.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
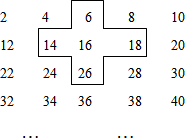 探索规律将连续的偶2,4,6,8,…,排成如表:
探索规律将连续的偶2,4,6,8,…,排成如表:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
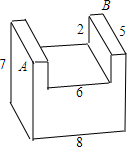 在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是13分米.
在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是13分米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
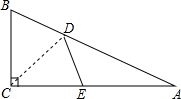 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )| A. | 46° | B. | 60° | C. | 68° | D. | 77° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
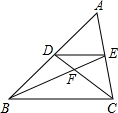 如图,在△ABC中,D、E分别为AB,AC的中点,连接BE,DC交于F点,则△DEF与△BDF的面积比为( )
如图,在△ABC中,D、E分别为AB,AC的中点,连接BE,DC交于F点,则△DEF与△BDF的面积比为( )| A. | 1:2 | B. | 1:4 | C. | 4:9 | D. | 1:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
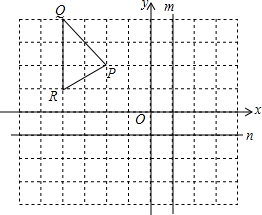 如图,每个正方形的边长都是1,分别作出△PQR关于直线x=1(记为m)和直线y=-1(记为n)对称的图形,它们的对应点的坐标之间分别有什么关系?
如图,每个正方形的边长都是1,分别作出△PQR关于直线x=1(记为m)和直线y=-1(记为n)对称的图形,它们的对应点的坐标之间分别有什么关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com