
【题目】如图,抛物线y=ax2+bx+c过原点O、点A (2,﹣4)、点B (3,﹣3),与x轴交于点C,直线AB交x轴于点D,交y轴于点E.
(1)求抛物线的函数表达式和顶点坐标;
(2)直线AF⊥x轴,垂足为点F,AF上取一点G,使△GBA∽△AOD,求此时点G的坐标;
(3)过直线AF左侧的抛物线上点M作直线AB的垂线,垂足为点N,若∠BMN=∠OAF,求直线BM的函数表达式.
【答案】解:(1)∵将原点O、点B、点C的坐标代入得: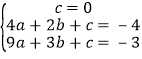 ,解得:a=1,b=﹣4,c=0,
,解得:a=1,b=﹣4,c=0,
∴抛物线的解析式为y=x2﹣4x.
(2)设直线AB的解析式为y=kx+b.
∵将点A(2,﹣4)、B(3,﹣3)代入得![]() ,解得:k=1,b=﹣6,
,解得:k=1,b=﹣6,
∴直线AB的解析式为y=x﹣6.
∵令y=0得x﹣6=0,解得:x=6,
∴D(6,0).
∴OD=6.
∵AF⊥x轴,(2,﹣4),
∴F(2,0).
∴AF=4,DF=4.
∴AF=DF.
∴∠GAB=∠ODA.
∴当![]() 时,△GBA∽△AOD.
时,△GBA∽△AOD.
∵由两点间的距离公式可知AB=![]() =
=![]() ,AD=
,AD=![]() =4
=4![]() ,
,
∴![]() ,解得;AG=
,解得;AG=![]() .
.
∴G(2,﹣![]() ).
).
(3)如图1所示:BM与AF的交点记为G.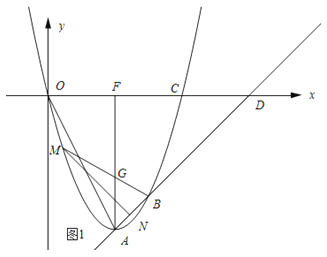
∵∠BMN=∠OAF,∠A=∠ODA,
∴△GBA∽△AOD.
∴![]() ,即
,即![]() ,解得;AG=
,解得;AG=![]() .
.
∴G(2,﹣![]() ).
).
设直线BM的解析式为y=kx+b.
∵将点B、G的坐标代入得: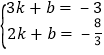 ,解得:k=﹣
,解得:k=﹣![]() ,b=﹣2.
,b=﹣2.
∴直线BM的解析式为y=﹣![]() X﹣2.
X﹣2.
如图2所示:MB与x交点记为G.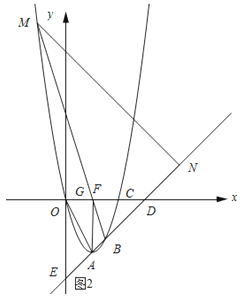
BD=AD﹣AB=4![]() ﹣
﹣![]() =3
=3![]() .
.
∵∠BMN=∠OAF,∠GDB=∠ODA,
∴△FBD∽△AOD.
∴![]() ,即
,即![]() ,解得DG=4.
,解得DG=4.
∴点G的坐标为(2,0).
设直线BM的解析式为y=kx+b.
∵将点B和点G的坐标代入得:![]() ,解得k=﹣3,b=6.
,解得k=﹣3,b=6.
∴直线BM的解析式为y=﹣3x+6.
综上所述,直线MB的解析式为y=-![]() x﹣2或y=﹣3x+6.
x﹣2或y=﹣3x+6.
【解析】(1)将原点O、点B、点C的坐标代入求得a、b、c的值即可;
(2)先求得直线AB的解析式,然后可求得点D的坐标,于是得到AF=DF,由两点间的距离公式可求得AB、AD的长,由等腰三角形的性质可证明∠GAB=∠ODA,故此![]() 时,△GBA∽△AOD.接下来依据关系式可求得AG的长,从而可求得点G的坐标;
时,△GBA∽△AOD.接下来依据关系式可求得AG的长,从而可求得点G的坐标;
(3)如图1所示:BM与AF的交点记为G.先证明△GBA∽△AOD,由相似三角形的性质可求得AG的长,于是得到点G的坐标,然后依据待定系数法可求得BM的解析式;如图2所示:MB与x交点记为G.先证明△FBD∽△AOD,由相似三角形的性质可求得DG的长,从而得到点G的坐标,然后依据待定系数法可求得MB的解析式


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A,B为圆心,大于![]() AB的长为半径作弧,两弧在直线AB两侧分别交于M,N两点,过M,N作直线交AB于点P,交AC于点D,连结BD.下列结论中,错误的是( )
AB的长为半径作弧,两弧在直线AB两侧分别交于M,N两点,过M,N作直线交AB于点P,交AC于点D,连结BD.下列结论中,错误的是( )
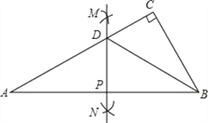
A. 直线AB是线段MN的垂直平分线 B. CD=![]() AD
AD
C. BD平分∠ABC D. S△APD=S△BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFl,得到图②.
(1)在图①中,过点P作PM∥AB,当α=20°,β=50°时,∠EPM= 度,∠EPF= 度;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请直接写出α与β的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
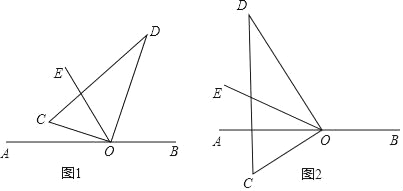
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策,各地政府高度重视、积极响应,中国掀起了大众创业万众创新的新浪潮.某创新公司生产营销A、B两种新产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系y=ax2+bx,当x=1时,y=7;当x=2时,y=12.
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求a,b的值;
(2)该公司准备生产营销A、B两种产品共10吨,请设计一个生产方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
(1)若MA=2,求C点的坐标;
(2)若D点的坐标为(4,0),求MC的长;
(3)当OF=MA时,直接写出点M的坐标.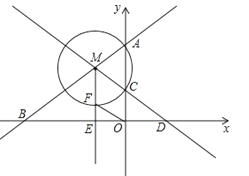
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
A.![]() >4ac
>4ac
B.m>n
C.方程a![]() +bx+c=﹣4的两根为﹣5或﹣1
+bx+c=﹣4的两根为﹣5或﹣1
D.a![]() +bx+c≥﹣6
+bx+c≥﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com