
����Ŀ����ͼ�٣���֪AB��CD����E��F�ֱ���AB��CD�ϵĵ㣬��P����ƽ����֮���һ�㣬���AEP=������PFC=������ͼ���У�����E������EH��CD�ڵ�N��������FI���ӳ�PF��G��ʹ��PE��FG�ֱ�ƽ�֡�AEH����DFl���õ�ͼ����
��1����ͼ���У�����P��PM��AB������=20�㣬��=50��ʱ����EPM=�� ���ȣ���EPF=�� ���ȣ�
��2���ڣ�1���������£���ͼ���С�END���CFI�Ķ�����
��3����ͼ���У���FI��EHʱ����ֱ��д����������������ϵ��

���𰸡���1��20��70����2��80�㣻��3��90�㣻
��������
��1����PM��AB������ֱ��ƽ�У��ڴ�����ȿɵá�EPM=��AEP=20�㣬����ƽ�й��������ۿɵ�PM��CD���̶��ɵá�MPF=��CFP=50�㣬�Ӷ�������á�EPF��
��2���ɽ�ƽ���ߵĶ���ɵá�AEH=2��=40�㣬�ٸ���AD��BC������ֱ��ƽ�У��ڴ�����ȿɵá�END=��AEH=40�㣬�ɶԶ�������Լ���ƽ���߶���ɵá�IFG=��DFG=��=50�㣬�ٸ���ƽ�Ƕ��弴����á�CFI�Ķ�����
��3���ɣ�2���ɵã���CFI=180��-2�£���AB��CD���ɵá�END=2������FI��EHʱ����END=��CFI���ݴ˼��ɵ���+��=90�㣮
��1����PM��AB����=20�㣬
���EPM=��AEP=20�㣬
��AB��CD��PM��AB��
��PM��CD��
���MPF=��CFP=50�㣬
���EPF=20��+50��=70�㣬
�ʴ�Ϊ��20��70��
��2����PEƽ�֡�AEH��
���AEH=2��=40�㣬
��AD��BC��
���END=��AEH=40�㣬
�֡�FGƽ�֡�DFI��
���IFG=��DFG=��=50�㣬
���CFI=180��-2��=80�㣻
��3���ɣ�2���ɵã���CFI=180��-2�£�
��AB��CD��
���END=��AEN=2����
�൱FI��EHʱ����END=��CFI��
��2��=180��-2�£�
����+��=90�㣮


 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У�ADƽ�֡�BAC��AD��BC������ΪD��AN����ABC��ǡ�CAM��ƽ���ߣ�CE��AN������ΪE.
��1����֤���ı���ADCE�Ǿ��Σ�
��2������ABC����ʲô����ʱ���ı���ADCE�������Σ�����֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x�ķ�ʽ����![]() ��3��
��3��![]() �и������⣬�ҹ���x�IJ���ʽ��
�и������⣬�ҹ���x�IJ���ʽ��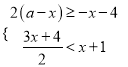 �Ľ⼯Ϊx����2����ô������������������a�Ļ���_________��
�Ľ⼯Ϊx����2����ô������������������a�Ļ���_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����E��F�ֱ���AB��AC�ϣ�AE=AF��BF��CE�ཻ�ڵ�P����֤��PB=PC����ֱ��д��ͼ��������ȵ��߶Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��E�ֱ���AB��BC�ϵĵ㣬��DE��AC����S��BDE��S��CDE=1��4����S��BDE��S��ACD=��������
A.1��16
B.1��18
C.1��20
D.1��24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A��90����AB��AC��O��BC���е㣬�����AB��AC�Ϸֱ���һ������M��N���ƶ��������ƶ�ʱ����AN��BM�������ж���OMN����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ɫ�����߲˻����мס�������ֲ������������ֲ��A��B�����߲ˣ�����ֲ����ֲ�������߲˵���ֲ��������������±���
��ֲ�� | ��ֲA���߲��������λ��Ķ�� | ��ֲB���߲��������λ��Ķ�� | �����루��λ��Ԫ�� |
�� | 1 | 3 | 13500 |
�� | 2 | 2 | 13000 |
˵������ͬ��ֲ����ֲ��ͬ���߲�ÿĶƽ���������
��1����A��B�����߲�ÿĶƽ��������Ƕ���Ԫ��
��2������ס�������ֲ��������ֲ���ƻ�����50Ķ��������ֲA��B�����߲ˣ�Ϊ��ʹ�����벻����16400Ԫ����������ֲ��������ֲA���߲˶���Ķ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��ԭ��O����A ��2����4������B ��3����3������x�ύ�ڵ�C��ֱ��AB��x���ڵ�D����y���ڵ�E��
��1���������ߵĺ�������ʽ�Ͷ������ꣻ
��2��ֱ��AF��x�ᣬ����Ϊ��F��AF��ȡһ��G��ʹ��GBA�ס�AOD�����ʱ��G�����ꣻ
��3����ֱ��AF�����������ϵ�M��ֱ��AB�Ĵ��ߣ�����Ϊ��N������BMN=��OAF����ֱ��BM�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ϧ������ע�ⰲȫ����һ����Ļ��⣮���ִ����ij��У���ͨ��ȫ�����ܱ����ӣ����м���ͼ���ǹ���ͨ�õļ��ֽ�ͨ��־�����в������ĶԳ�ͼ���ǣ�������
A.��ֹ�г�
B.��ֹ����ͨ��
C.��ֹ������ʱ��ͣ��
D.��ֹ������ʱ��ʱ��ͣ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com