
【题目】如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM,请你判断△OMN的形状,并说明理由.

【答案】△OMN是等腰直角三角形.理由见解析.
【解析】
试题分析:连接OA.先证得△OAN≌△OBM,然后根据全等三角形的对应边相等推知OM=ON;然后由等腰直角三角形ABC的性质、等腰三角形OMN的性质推知∠NOM=90°,即△OMN是等腰直角三角形.
试题解析:△OMN是等腰直角三角形.
理由:连接OA.
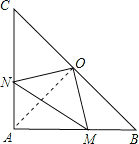
∵在△ABC中,∠A=90°,AB=AC,O是BC的中点,
∴AO=BO=CO(直角三角形斜边上的中线是斜边的一半);
∠B=∠C=45°;
在△OAN和OBM中,
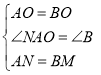
∴△OAN≌△OBM(SAS),
∴ON=OM;
∴∠AON=∠BOM;
又∵∠BOM+∠AOM=90°,
∴∠NOM=∠AON+∠AOM=90°,
∴△OMN是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
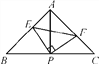
【题目】如图,△ABC中,AB=AC,∠BAC=90°,P是BC中点,∠EPF=90°,给出四个结论:①∠B=∠BAP;②AE=CF;③PE=PF;④S四边形AEPF=![]() S△ABC.其中成立的有_______
S△ABC.其中成立的有_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC的两条高AD、BE相交于点H,且AD=BD,试说明下列结论成立的理由。(1)∠DBH=∠DAC;(2)△BDH≌△ADC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFl,得到图②.
(1)在图①中,过点P作PM∥AB,当α=20°,β=50°时,∠EPM= 度,∠EPF= 度;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请直接写出α与β的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.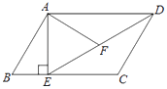
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3![]() , AF=2
, AF=2![]() , 求AE的长.
, 求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
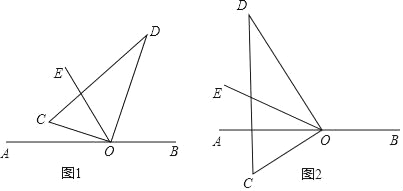
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
(1)若MA=2,求C点的坐标;
(2)若D点的坐标为(4,0),求MC的长;
(3)当OF=MA时,直接写出点M的坐标.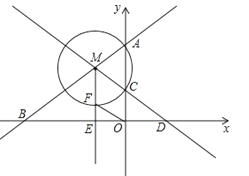
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com