
【题目】如图,正方形ABCD的两个顶点A , D分别在x轴和y轴上,CE⊥y轴于点E , OA=2,∠ODA=30°.若反比例函数y= ![]() 的图象过CE的中点F , 则k的值为 .
的图象过CE的中点F , 则k的值为 . 
【答案】6+2 ![]()
【解析】
解:在正方形ABCD中,AD=CD , ∠CDA=90度,
则∠ADO+∠CDE=90度,
又因为∠ADO+∠OAD=90度,
所以∠CDE=∠OAD ,
在△ADO和△DCE中,
∠CED=∠AOD , ∠CDE=∠OAD , AD=CD ,
所以△ADO△DCE(AAS),
所以DO=CE , AO=DE ,
在Rt△ADO中,因为OA=2 , ∠ODA=30° .
所以DO=![]() OA=2
OA=2![]() , AD=2OA=4 ,
, AD=2OA=4 ,
则OE=DO+DE=DO+AO=2![]() +2 ,
+2 ,
即C(2![]() , 2
, 2![]() +2),
+2),
因为F是CE的中点,且CE//x轴,
所以F(![]() , 2
, 2![]() +2),
+2),
将F(![]() , 2
, 2![]() +2),代入反比例函数
+2),代入反比例函数![]() ,
,
得k=![]() (2
(2![]() +2).
+2).
所以答案是6+2![]() 。
。
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1 , y1)、N(x2 , y2)是反比例函数y=![]() 图象上的两点,且x1<x2 , y1<y2 , 指出点M、N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2 , y1<y2 , 指出点M、N各位于哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点. 
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)如图②,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图③,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE与△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
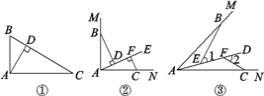
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数 ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4 ![]()
C.12-3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',C=∠C'=90°.
求证:Rt△ABC和Rt△A'B'C'全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A'B'C'拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A'重合,点C与点C'重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com