Question

【题目】如图1，在平面直角坐标系中，AB⊥x轴于B，AC⊥y轴于C，点C(0，4)，A(4，4)，过C点作∠ECF分别交线段AB、OB于E、F两点.

（1）若OF+BE=AB，求证：CF=CE.

（2）如图2，∠ECF=45°， S△ECF=6，求S△BEF的值.

Answer 1

【答案】（1）见解析；（2）S△BEF的值为4.

【解析】

（1）根据条件证出四边形ABOC是正方形，然后证明△COF≌△CAE即可；

（2）在x轴上截取OG=AE，连接CG，证明△COG≌△CAE，进而证出△GCF≌△ECF，根据全等三角形的面积相等得出S△COF+S△ACE =6，然后利用S△BEF=S四边形ABOC-（S△COF+S△ACE+S△ECF）计算即可．

（1）证明：∵AB⊥x轴，AC⊥y轴，A（4，4），

∴AB=AC=OC=OB，∠ACO=∠COB=∠ABO=90°，

又∵四边形的内角和是360°，

∴∠A=90°，

∵OF+BE=AB=BE+AE，

∴AE=OF，

∴在△COF和△CAE中，

，

∴△COF≌△CAE（SAS），

∴CF=CE；

（2）在x轴上截取OG=AE，连接CG，

在△COG和△CAE中，

，

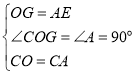∴△COG≌△CAE（SAS），

∴CG=CE，∠GCO=∠ACE，

∵∠ECF=45°，

∴∠ACE+∠FCO=∠ACO-∠ECF=45°，

∴∠GCF=∠GCO+∠FCO=∠ACE+∠FCO=45°，

∴∠GCF=∠ECF，

在△GCF和△ECF中，

，

∴△GCF≌△ECF（SAS），

∴S△GCF=S△ECF=6，

∵S△COG=S△ACE，

∴S△COF+S△ACE= S△COF +S△COG=S△GCF=6，

∵S四边形ABOC=16，

∴S△BEF=S四边形ABOC-（S△COF+S△ACE+S△ECF）=4．