【题目】如图，点A、B是反比例函数y＝
图象上的两点，已知点B的坐标为（3，2），△AOB的面积为2.5，求该反比例函数的解析式和点A的坐标．
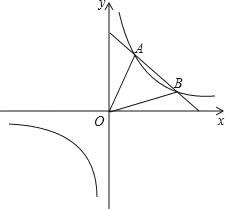
【答案】反比例函数的解析式是y＝
，点A的坐标是（2，3）．
【解析】
把点B的坐标代入函数解析式可以求得k的值．如图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D．则S△AOB＝S梯形ACDB，据此可以求得点A的坐标．
把点B的坐标（3，2）代入y＝
，得
k＝xy＝3×2＝6，
则该反比例函数为解析式为：y＝
．
如图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D．
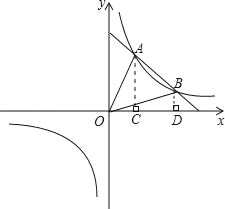
设A（a，
）．
∵点A、B是反比例函数y＝图象上的两点，
∴S△AOC＝S△BOD，
∴S△AOB＝S△AOC+S梯形ACDB﹣S△BOD＝S梯形ACDB，
则2.5＝
×（3﹣a），
整理，得
（a﹣2）（a+9）＝0，
解得a1＝2，a2＝﹣9（舍去）．
则A（2，3）．
综上所述，该反比例函数的解析式是y＝，点A的坐标是（2，3）．
科目：初中数学 来源： 题型：
【题目】关于三角函数有如下的公式：
sin（α+β）=sinαcosβ+cosαsinβ①
cos（α+β）=cosαcosβ﹣sinαsinβ②
tan（α+β）=
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值，如：
tan105°=tan（45°+60°）=
=﹣（2+
）．
根据上面的知识，你可以选择适当的公式解决下面的实际问题：
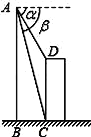
如图，直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°，底端C点的俯角β=75°，此时直升飞机与建筑物CD的水平距离BC为42m，求建筑物CD的高．
查看答案和解析>>
科目：初中数学 来源： 题型：
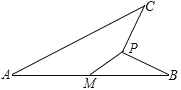
【题目】如图，线段 AB＝4，M 为 AB 的中点，动点 P 到点 M 的距离是 1，连接 PB，线段
PB 绕点 P 逆时针旋转 90°得到线段 PC，连接 AC，则线段 AC 长度的最大值是_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
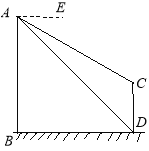
【题目】如图，AB、CD为两个建筑物，建筑物AB的高度为60米，从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°，测得建筑物CD的底部D点的俯角∠EAD为45°．
（1）求两建筑物底部之间水平距离BD的长度；
（2）求建筑物CD的高度（结果保留根号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
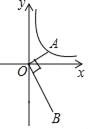
【题目】如图，已知点A是反比例函数y＝
（x＞0）的图象上的一个动点，连接OA，OB⊥OA，且OB＝2OA，那么经过点B的反比例函数图象的表达式为（ ）
A. y＝﹣
B. y＝ C. y＝﹣
D. y＝
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有四部不同的电影，分别记为A、B、C、D．
（1）若甲从中随机选择一部观看，则恰好是电影A的概率是 ；
（2）若甲从中随机选择一部观看，乙也从中随机选择一部观看，用列表或画树状图的方法列出所有等可能的结果，并求甲、乙两人恰好选择同一部电影的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知二次函数
（a＞0）图像与x轴交于点A、B（点A在点B的左侧），与y轴的交于点C，顶点为D ．
（1）求点A、B的坐标；
（2）若M为对称轴与x轴交点，且DM=2AM，
①求二次函数解析式；
②当30°＜∠ADM＜45°时，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若一组数据a，b，c的平均数为5，方差为4，那么数据a+2，b+2，c+2的平均数和方差分别是( )
A.5，4B.4，5C.7，4D.7，3
查看答案和解析>>
科目：初中数学 来源： 题型：
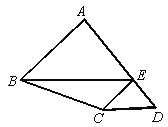
【题目】如图，在四边形ABCD 中，点E在AD上，EC∥AB，EB∥DC，若△ABE面积为5，△ECD的面积为1，则△BCE的面积是__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com