
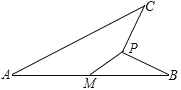
【题目】如图,线段 AB=4,M 为 AB 的中点,动点 P 到点 M 的距离是 1,连接 PB,线段
PB 绕点 P 逆时针旋转 90°得到线段 PC,连接 AC,则线段 AC 长度的最大值是_________.
【答案】3![]()
【解析】
以O为坐标原点建立坐标系,过点C作CD⊥y轴,垂足为D,过点P作PE⊥DC,垂足为E,延长EP交x轴于点F,设点P的坐标为(x,y),根据题意动点 P 到点 M 的距离是 1,在△0PF中利用勾股定理得x2+y2=1.然后证明△ECP≌△FPB,由全等三角形的性质得到EC=PF=y,FB=EP=2-x,从而得到点C(x+y,y+2-x),最后依据两点间的距离公式可求得AC=![]() ,最后,依据当y=1时,AC有最大值求解即可.
,最后,依据当y=1时,AC有最大值求解即可.
解:如图所示:过点C作CD⊥y轴,垂足为D,过点P作PE⊥DC,垂足为E,延长EP交x轴于点F.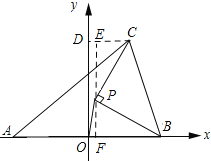
∵AB=4,O为AB的中点,
∴A(-2,0),B(2,0).
设点P的坐标为(x,y),则x2+y2=1.
∵∠EPC+∠BPF=90°,∠EPC+∠ECP=90°,
∴∠ECP=∠FPB.
由旋转的性质可知:PC=PB.
在△ECP和△FPB中,
 ,
,
∴△ECP≌△FPB.
∴EC=PF=y,FB=EP=2-x.
∴C(x+y,y+2-x).
∵AB=4,O为AB的中点,
∴AC=![]() =
=![]()
∵x2+y2=1,
∴AC=![]()
∵-1≤y≤1,
∴当y=1时,AC有最大值,AC的最大值为![]() =3
=3![]() .
.
故答案为:3![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某工人打算用不锈钢条加工一个面积为0.8平方米的矩形模具.假设模具的长与宽分别为x米和y米.
(1)你能写出y与x之间的函数解析式吗?
(2)变量y与x是什么函数关系?
(3)已知这种不锈钢条每米6元,若想使模具的长比宽多1.6米,则加工这个模具共需花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假定甲、乙两人在一次赛跑中,路程S与时间T的关系在平面直角坐标系中如图所示,请结合图形和数据回答问题:
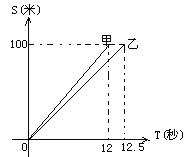
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)乙在这次赛跑中的速度为 ;
(4)甲到达终点时,乙离终点还有 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
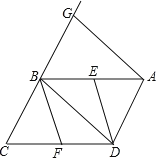
【题目】已知:如图,在平行四边形![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,连接
的中点,连接![]() ,作
,作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(1)求证:![]() ;
;
(2)若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 是什么特殊四边形?证明你的结论.
是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在矩形ABCD中,EF经过对角线BD的中点O,并交AD,BC于点E,F.

(1)求证:△BOF≌△DOE
(2)若AB=4cm,AD=5cm,求四边形ABFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
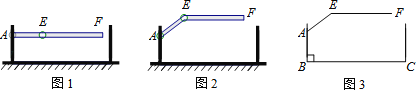
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
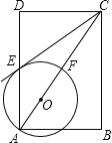
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若AB=2,BC=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com