
【题目】如图:在矩形ABCD中,EF经过对角线BD的中点O,并交AD,BC于点E,F.

(1)求证:△BOF≌△DOE
(2)若AB=4cm,AD=5cm,求四边形ABFE的面积.
科目:初中数学 来源: 题型:
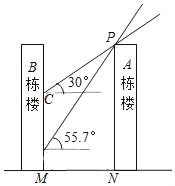
【题目】如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为![]() ”是随机事件;
”是随机事件;
B. 某种彩票的中奖率是![]() ,说明每买100张彩票,一定有1张中奖;
,说明每买100张彩票,一定有1张中奖;
C. “篮球队员在罚球线上投篮一次,投中”为随机事件;
D. 投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程,解答后面的问题:
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 点的坐标;
点的坐标;
解:分别过![]() ,
,![]() 做
做![]() 轴的平行线,过
轴的平行线,过![]() ,
,![]() 做
做![]() 轴的平行线,两组平行线的交点如图
轴的平行线,两组平行线的交点如图![]() 所示,设
所示,设![]() ,则
,则![]() ,
,![]() ,
,![]()
由图![]() 可知:
可知:
![]()
![]()
![]() 线段
线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]()
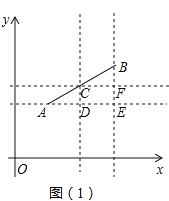
(应用新知)
利用你阅读获得的新知解答下面的问题:
(1)已知![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为
(2)平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,利用中点坐标公式求点
,利用中点坐标公式求点![]() 的坐标。
的坐标。
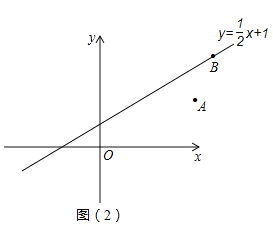
(3)如图![]() ,点
,点![]() 在函数
在函数![]() 的图象上,
的图象上, ![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() 在函数
在函数![]() 的图象上 ,以
的图象上 ,以![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点,且以
四个点为顶点,且以![]() 为一边构成平行四边形,直接写出所有满足条件的
为一边构成平行四边形,直接写出所有满足条件的![]() 点坐标。
点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
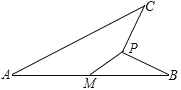
【题目】如图,线段 AB=4,M 为 AB 的中点,动点 P 到点 M 的距离是 1,连接 PB,线段
PB 绕点 P 逆时针旋转 90°得到线段 PC,连接 AC,则线段 AC 长度的最大值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
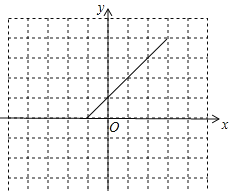
【题目】我们知道,把直线y=x向左平移1个单位可得到一次函数y=x+1的图象,把直线y=kx(k≠0)向左平移1个单位可得到一次函数y=k(x+1)的图象,把抛物线y=ax2(a≠0)向左平移1个单位,可得到二次函数y=a(x+1)2的图象.类似的:我们将函数y=∣x∣向左平移1个单位,在平面直角坐标系中画出了新函数的部分图象,并请回答下列问题:
(1)平移后的函数解析式是__________;
(2)借助下列表格,用你认为最简单的方法补画平移后的函数图象:
(3)当x 时,y随x的增大而增大;当x 时,y随x的增大而减小.
查看答案和解析>>
科目:初中数学 来源: 题型:
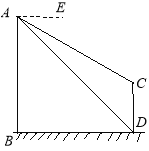
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四部不同的电影,分别记为A、B、C、D.
(1)若甲从中随机选择一部观看,则恰好是电影A的概率是 ;
(2)若甲从中随机选择一部观看,乙也从中随机选择一部观看,用列表或画树状图的方法列出所有等可能的结果,并求甲、乙两人恰好选择同一部电影的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4![]() ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )

A. (0,0) B. (1,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com