
如图:在长方形ABCD中, AB=CD=4cm,BC=3cm,动点P从点A出发,先以1cm/s的速度沿A→B,然后以2cm/s的速度沿B→C运动,到C点停止运动,设点P运动的时间为t秒,是否存在这样的t,使得△BPD的面积S>3cm2?如果能,请求出t的取值范围;如果不能,请说明理由.

存在这样的t,使得△BPD的面积满足条件,此时0≤t<2;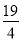 <t≤5.5.
<t≤5.5.
【解析】
试题分析:分两段考虑:①点P在AB上,②点P在BC上,分别用含t的式子表示出△BPD的面积,再由S>3cm2建立不等式,解出t的取值范围值即可.
试题解析:①当点P在AB上时,假设存在△BPD的面积满足条件,即运动时间为t秒,则
S△BPD=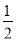 (4-t)×3=
(4-t)×3=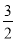 (4-t)>3
(4-t)>3
解得t<2,
又因为P在AB上运动,0≤t≤4,
所以0≤t<2;
②当点P在BC上时,假设存在△BPD的面积满足条件,即运动时间为t秒,则
S△BPD=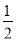 (4-t)×2×4=4t-16>3
(4-t)×2×4=4t-16>3
解得t>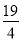 ,
,
又因为P在BC上运动,4<t≤5.5,
所以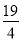 <t≤5.5;
<t≤5.5;
综上所知,存在这样的t,使得△BPD的面积满足条件,此时0≤t<2;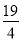 <t≤5.5.
<t≤5.5.
考点:一元一次不等式组的应用.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:2016届江苏省太仓市七年级下学期期末考试数学试卷(解析版) 题型:解答题
(1)解不等式:5(x-2)+8<7-6(x-1)
(2)若(1)中的不等式的最大整数解是方程2x-ax=3的解,求a的值.
查看答案和解析>>
科目:初中数学 来源:2016届江苏省南京市高淳区七年级下学期期中考试数学试卷(解析版) 题型:解答题
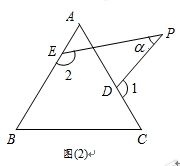
在等边△ABC中,点D、E分别是边AC、AB上的点(不与A、B、C重合),点P是平面内一动点。设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示.
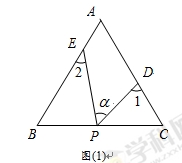
则∠1+∠2= .(用α的代数式表示)
(2)若点P在△ABC的外部,如图(2)所示.则∠α、∠1、∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边BC的延长线上运动时,试画出相应图形,并写出∠α、∠1、∠2之间的关系式.(不需要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com