
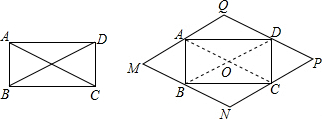
分析 如图,首先证明MN=2λ(设OB为λ),同理可证:PN=PQ=QM=2λ,得到四边形MNPQ的周长为8λ;解直角△ABC,求出AC=2λ=2,即可解决问题.
解答  解:如图,由题意得:
解:如图,由题意得:
∠ABM=∠ABO,∠NBC=∠OBC,
∴∠ABM+∠ABO+∠NBC+∠OBC=2∠ABC=180°,
∴M、B、N三点共线,
∴MN=MB+BN;
∵四边形ABCD为矩形,
∴OA=OB=OC=OD(设为λ);
由翻折变换的性质得:MB=BO,BN=BO,
∴MN=2λ,同理可证:PN=PQ=QM=2λ,
∴四边形MNPQ的周长=8λ;
在直角△ABC中,
∵OA=OB,∠AOB=60°,
∴△AOB为等边三角形,∠BAC=60°,
∴∠ACB=30°;而BC=$\sqrt{3}$,
∴AC=2λ=2,
∴四边形MNPQ的周长=8λ=8.
故答案为8.
点评 该题主要考查了翻折变换的性质、矩形的性质、等边三角形的判定、直角三角形的边角关系等几何知识点及其应用问题;灵活运用翻折变换的性质、矩形的性质等几何知识点是解题的关键.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
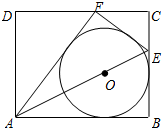 如图,四边形ABCD表示一张矩形纸片,AB=10,AD=8.E是BC上一点,将△ABE沿折痕AE向上翻折,点B恰好落在CD边上的点F处,⊙O内切于四边形ABEF.求:
如图,四边形ABCD表示一张矩形纸片,AB=10,AD=8.E是BC上一点,将△ABE沿折痕AE向上翻折,点B恰好落在CD边上的点F处,⊙O内切于四边形ABEF.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥3 | B. | a>3 | C. | a≤3 | D. | a<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
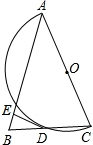 如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E
如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数是120 | B. | 方差是34 | C. | 中位数是135 | D. | 平均数是126 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com