
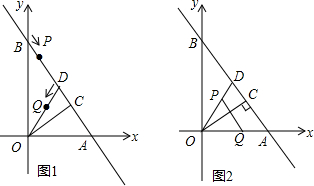
分析 (1)根据直线y=-$\sqrt{3}$x+2$\sqrt{3}$分别交x轴,y轴于点A、B,求出A与B点的坐标,得出AB的值,再根据D是AB的中点,即可求出OD的值;(2)过Q作QE⊥AB于E,可得QE∥OC,再由平行线分线段成比例定理,得到比例式$\frac{QE}{OC}=\frac{DQ}{DO}$,利用比例式将线段QE用含t的代数式表示,再根据S△DPQ=$\frac{1}{2}$DP•QE,即可求得S与t的函数关系式;(3)要使△OPE为等腰三角形,需分情况讨论:当PE=OE时,可得PQ∥OB,得出t-2=$\frac{1}{2}$(4-t),求出t的值;当OP=OE时,根据∠COD=30°,求出∠PQO=45°,过P作PF⊥OA,得出PF=QF,根据PF=cos30°×OP=$\frac{\sqrt{3}}{2}$(4-t),QF=t-2-$\frac{1}{2}$(4-t),得出t-2-$\frac{1}{2}$(4-t)=$\frac{\sqrt{3}}{2}$(4-t),求出t的值;当PO=PE时,得∠POE=∠PEO=30°,得出PE∥OA,此时△POE不存在,从而求出△OPE为等腰三角形时,t的值.
解答 解:(1)∵直线y=-$\sqrt{3}$x+2$\sqrt{3}$分别交x轴,y轴于点A、B,
∴令x=0得,y=2$\sqrt{3}$,令y=0得,-$\sqrt{3}$x+2$\sqrt{3}$=0,解得,x=2,
∴点B的坐标为:(0,2$\sqrt{3}$),点A的坐标为:(2,0),
∴线段OA=2,OB=2$\sqrt{3}$,
∴AB=4,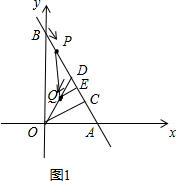
∵D是AB的中点,
∴OD是直角三角形AOB的斜边上的中线,
∴OD=2;
∵Rt△AOB,OC⊥AB,
∴AB•OC=AO•BO,
4OC=2$\sqrt{3}$×2,
∴OC=$\sqrt{3}$;
(2)过Q作QE⊥AB于E,如图1
∵OC⊥AB于点C,
∴QE∥OC,∴$\frac{QE}{OC}=\frac{DQ}{DO}$,
∵动点P从B出发沿折线BD→DO方向以每秒1个单位长度的速度向终点O运动,
动点Q从点D出发沿折线DO→OA方向以相同的速度运动,
∴DP=BD-BP=2-t,DQ=t,
∵OC=$\sqrt{3}$,
∴$\frac{QE}{\sqrt{3}}=\frac{t}{2}$,
∴QE=$\frac{\sqrt{3}t}{2}$,
∴S△DPQ=$\frac{1}{2}$DP•QE=$\frac{1}{2}$(2-t)•$\frac{\sqrt{3}t}{2}$=-$\frac{{\sqrt{3}t}^{2}}{4}$+$\frac{\sqrt{3}t}{2}$(0<t≤2).
(3)∵OD=0A=AD=2,
∴△AOD是等边三角形,
∴∠AOD=∠ADO=∠OAD=60°,
∴∠BOD=∠OBD=30°,
∵OC⊥AB于点C,
∴∠POE=30°,
①当PE=OE时,∠POE=∠OPE=30°
∴∠BOD=∠OPE,
∴PQ∥OB,
∴PQ⊥x轴,
∴OQ=$\frac{1}{2}$OP,即t-2=$\frac{1}{2}$(4-t),
∴t=$\frac{8}{3}$,
②当OP=OE时,∠OPE=∠OEP,
∵∠COD=30°,
∴∠OPQ=75°,
∴∠PQO=45°,
过P作PF⊥OA,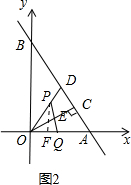
∴PF=QF,∠OPF=30°,
∴OF=$\frac{1}{2}$OP=$\frac{1}{2}$(4-t),
∵PF=cos30°×OP=$\frac{\sqrt{3}}{2}$(4-t),
QF=t-2-$\frac{1}{2}$(4-t),
∴t-2-$\frac{1}{2}$(4-t)=$\frac{\sqrt{3}}{2}$(4-t),
∴t=$\frac{2\sqrt{3}+6}{3}$,
③当PO=PE时,得∠POE=∠PEO=30°,
则PE∥OA,
此时△POE不存在,
所以此情况不成立,
综上当t=$\frac{8}{3}$或t=$\frac{2\sqrt{3}+6}{3}$时,△OPE为等腰三角形.
点评 本题考查了一次函数与坐标轴的交点坐标的求法,平行线的判定与性质,平行线分线段成比例定理,利用三角形的面积列函数关系式,直角三角形的性质,等腰三角形的性质、解直角三角形,能运用数形结合的思想和分类讨论的思想及综合运用所学是解题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①② | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F.G,则弧FG对的圆周角∠FPG的大小为( )
如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F.G,则弧FG对的圆周角∠FPG的大小为( )| A. | 45° | B. | 60° | C. | 75° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
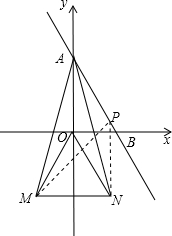 如图,直线y=kx+2(0<|k|≤1)分别与坐标轴交于A,B两点,等边△MNO关于y轴对称,点M(-1,$-\sqrt{3}$),P是直线AB上的动点.∠MAN度数为30°,当∠MPN=∠MAN时,点P的坐标为$(\frac{-4k}{{k}^{2}+1},\frac{2-2{k}^{2}}{{k}^{2}+1})$ (A点除外).
如图,直线y=kx+2(0<|k|≤1)分别与坐标轴交于A,B两点,等边△MNO关于y轴对称,点M(-1,$-\sqrt{3}$),P是直线AB上的动点.∠MAN度数为30°,当∠MPN=∠MAN时,点P的坐标为$(\frac{-4k}{{k}^{2}+1},\frac{2-2{k}^{2}}{{k}^{2}+1})$ (A点除外).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.039×101 | B. | 3.039×104 | C. | 3.039×105 | D. | 30.39×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该函数图象与x轴相交 | B. | 该函数图象与y轴相交 | ||
| C. | 该函数图象关于原点成中心对称 | D. | 该函数图象是轴对称图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com