
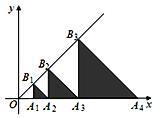
【题目】如图,△A1B1A2,△A2B2A3,△A3B3A4,...,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An,在x轴上,点B1、B2、…Bn在直线y=x上,已知OA1=1,则OA2019的长是_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
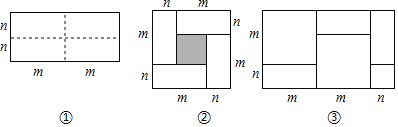
(1)图②中的阴影部分的面积为 .
(2)观察图②,三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 .
(3)若x+y=﹣6,xy=![]() ,则x﹣y= .
,则x﹣y= .
(4)观察图③,你能得到怎样的代数恒等式呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某销售商准备在南充采购一批丝绸,经调查,用10000元采购A型丝绸的件数与用8000元采购B型丝绸的件数相等,一件A型丝绸进价比一件B型丝绸进价多100元.
(1)求一件A型、B型丝绸的进价分别为多少元?
(2)若销售商购进A型、B型丝绸共50件,其中A型的件数不大于B型的件数,且不少于16件,设购进A型丝绸m件.
①求m的取值范围.
②已知A型的售价是800元/件,销售成本为2n元/件;B型的售价为600元/件,销售成本为n元/件.如果50≤n≤150,求销售这批丝绸的最大利润w(元)与n(元)的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科学技术的发展,信息化、网络化时代的到来,很多农产品改变了原来的销售模式,实行了网上销售,刚大学毕业的小韦把自己家的红薯产品也放到网上,他原来计划每天卖出150千克,由于各种原因,实际每天的销售量与计划量相比有出入,下表是国庆小长假期间的销售情况(超出部分记为正,不足记为负,单位:千克)
时间 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据上表前四天一共卖出了多少千克?
(2)销售量最多的一天与最少的一天分别是多少千克?
(3)若每千克按2. 6元出售,并需付运费平均每千克0. 3元,则小韦国庆小长假期间一共收入多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界卫生组织预计:到2025年,全世界将会有一半人面临用水危机,为了倡导“节约用水,从我做起”,某县政府决定对县直属机关300户家庭一年的月平均用水量进行调查,调查小组抽查了部分家庭月平均用水量(单位:吨),绘制条形图和扇形图如图所示.
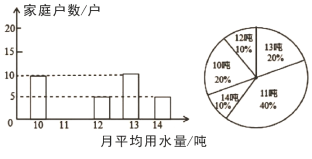
(1)请将条形统计图补充完整;
(2)这些家庭月平均用水量数据的平均数是_______,众数是______,中位数是_______;
(3)根据样本数据,估计该县直属机关300户家庭的月平均用水量不超过12吨的约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节期间某商场对顾客实行优惠,规定如下:若一次购物不超过 300 元(含 300 元),按标价九折优惠,若一次购物超过 300 元,但不超过 800 元(含 800 元),所有商品按标价给予八折优惠,若一次购物超过 800 元,其中 800 元按八折优惠之外,超过 800 元的部分给予六折优惠.
(1)若某人一次购物货款为x元(x>1000),打折后应付多少元?
(2)若某人两次购物分别付款180 元和 1000 元,如果他合起来一次去购买同样的商品,他还可以节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
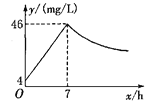
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com