Question

10．已知∠AOB内一点C关于OA、OB的对称点分别为D、E，若∠AOB=30°，则△DOE是等边三角形．

Answer 1

分析 根据题意画出草图，根据轴对称的性质求得OE=CO=OD，∠EOD=60°，即可判断△DOE为等边三角形．

解答 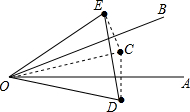解：根据题意画出图形：
∵C关于OA、OB的对称点分别为D、E
∴AO⊥CD，CO=OD
BO⊥EC，OE=OC
∴△EOC为等腰三角形
△COD为等腰三角形
∴∠EOC=∠COB，∠COA=∠AOD，OE=OC=OD
又∵∠AOB=30°
∴∠BOC+∠AOC=30°
∴∠BOE+∠AOD=30°
∴∠EOD=60°
又∵EO=OD
∴△EOD为等边三角形．
故答案为：等边．

点评 本题考查了轴对称的性质以及等边三角形的判定及性质．关键要理解有一个角为60°的等腰三角形是等边三角形，其中60°可以是顶角，也可以是底角．