
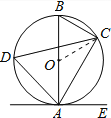
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.

(1)、求∠D的度数;
(2)、当BC=4时,求劣弧AC的长.
【答案】(1)、60°;(2)、![]() .
.
【解析】
试题分析:(1)、根据切线的性质得出∠BAE=90°,根据∠BAC=∠BAE﹣∠CAE,求出∠BAC的度数,再根据AB是⊙O的直径,得出∠ABC=90°,求出∠B的度数,再根据∠D=∠B,即可得出∠D的度数;(2)、连接OC,根据OB=OC,∠B=60°,得出△OBC是等边三角形,求出OB=BC=4,∠BOC=60°,从而得出∠AOC=120°,再根据弧长公式即可得出答案.
试题解析:(1)、∵AE是⊙O的切线, ∴AB⊥AE, ∴∠BAE=90°, ∵∠CAE=60°,
∴∠BAC=∠BAE﹣∠CAE=90°﹣60°=30°, ∵AB是⊙O的直径, ∴∠ABC=90°, ∴∠B=60°,
∵∠D=∠B, ∴∠D=60°
(2)、连接OC, ∵OB=OC,∠B=60°, ∴△OBC是等边三角形, ∵BC=4, ∴OB=BC=4,∠BOC=60°,
∴∠AOC=120°, ∴劣弧AC的长是:![]() .
.


科目:初中数学 来源: 题型:
【题目】我国计划在2020年左右发射火星探测卫星,据科学研究测量,火星距离地球的最近距离约为5500万千米,这个数据用科学计数法表示为
A. 5.5×106 B. 5.5×107 C. 55×107 D. 0.55×108
查看答案和解析>>
科目:初中数学 来源: 题型:
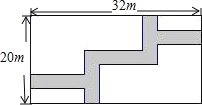
【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.

(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值;若不存在,请说明理由;
(3)△OPD为等腰三角形时,写出点P的坐标(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进江南新区的发展,長江三桥在区政府的统一指导下夜以继日的修建中,为方便残疾人通行,政府计划在位于南滨路桥头处修建一锲形残疾人通道,如图,该楔形斜坡BC长20米,坡角为12°,区领导为进一步方便残疾人的轮椅车通行,准备把坡角降为5°.

(1)求斜坡新起点到原起点B的距离(精确到0.1米)
(参考数据:sin12°≈0.21,cos12°≈0.98,tan5°≈0.09)
(2)某6人工程队承担这项改进任务(假设每人毎天的工怍效率相同),5天刚好完成该项工程;但实际工作
2天后.有2人因其它工作调离;剩余的工程由余下的4人独自完成,为了不延误工期,每人的工作效率提高了a%,结果准时完成该项工程,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)|﹣2|﹣(2﹣π)0+![]() +(﹣2)3
+(﹣2)3
(2)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(3)(x+y)2(x﹣y)2
(4)(x﹣2y+3z)(x+2y﹣3z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com