
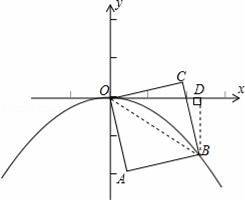
如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为 .


﹣
 .
.
【考点】二次函数综合题.
【专题】压轴题.
【分析】连接OB,根据正方形的对角线平分一组对角线可得∠BOC=45°,过点B作BD⊥x轴于D,然后求出∠BOD=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得BD=
 OB,再利用勾股定理列式求出OD,从而得到点B的坐标,再把点B的坐标代入抛物线解析式求解即可.
OB,再利用勾股定理列式求出OD,从而得到点B的坐标,再把点B的坐标代入抛物线解析式求解即可.
【解答】解:如图,连接OB,
∵四边形OABC是边长为1的正方形,
∴∠BOC=45°,OB=1×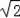
 =
=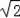
 ,
,
过点B作BD⊥x轴于D,
∵OC与x轴正半轴的夹角为15°,
∴∠BOD=45°﹣15°=30°,
∴BD=
 OB=
OB=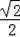
 ,
,
OD=
 =
=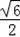
 ,
,
∴点B的坐标为(
 ,﹣
,﹣
 ),
),
∵点B在抛物线y=ax2(a<0)的图象上,
∴a(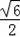
 )2=﹣
)2=﹣
 ,
,
解得a=﹣
 .
.
故答案为:﹣
 .
.

【点评】本题是二次函数综合题型,主要利用了正方形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理的应用,二次函数图象上点的坐标特征,熟记正方形性质并求出OB与x轴的夹角为30°,然后求出点B的坐标是解题的关键.


科目:初中数学 来源: 题型:
某品牌专卖店对上个月销售的男运动靯尺码统计如下, 这组统计数据中的众数是_______码.
| 码号(码) | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| 销售量(双) | 6 | 8 | 14 | 20 | 17 | 3 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程(a﹣c)x2﹣2bx+(a+c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校要从九年级(一)班和(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
 (一)班:168 167 170 165 168 166 171 168 167 170
(一)班:168 167 170 165 168 166 171 168 167 170
(二)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表
| 班级 | 平均数 | 方差 | 中位数 |
| 一班 | 168 | 168 | |
| 二班 | 168 | 3.8 |
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知样本甲平均数 ,方差
,方差 ,样本乙的平均数
,样本乙的平均数 ,方差
,方差 ,那么两个样本波
,那么两个样本波 动的情况为( )
动的情况为( )
A. 甲乙两样本波动一样大 B. 甲样本波动比乙样本大
C. 乙样本波动比甲样本 大 D. 无法比较两样本的波动大小
大 D. 无法比较两样本的波动大小
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
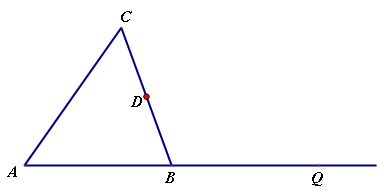
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com