
【题目】﹣14+3tan30°﹣ ![]() +(2017+π)0+(
+(2017+π)0+( ![]() )﹣2 .
)﹣2 .
【答案】解:﹣14+3tan30°﹣ ![]() +(2017+π)0+(
+(2017+π)0+( ![]() )﹣2
)﹣2
=﹣1+3× ![]() ﹣
﹣ ![]() +1+4
+1+4
=4+ ![]() ﹣
﹣ ![]()
=4
【解析】先依据有理数的乘方法则、特殊锐角三角函数值、零指数幂的性质、负整数指数幂的性质进行化简,然后再依据实数的运算法则进行计算即可.
【考点精析】关于本题考查的零指数幂法则和整数指数幂的运算性质,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,是由一些棱长都为1的小正方体组合成的简单几何体.

![]() 该几何体的表面积
该几何体的表面积![]() 含下底面
含下底面![]() 为______;
为______;
![]() 请画出这个几何体的三视图并用阴影表示出来;
请画出这个几何体的三视图并用阴影表示出来;
![]() 如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: ![]() 的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)
的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)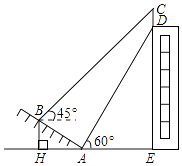
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m). (参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)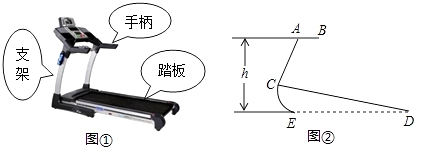
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年奥运会期间,一辆大巴车在一条南北方向的道路上来回运送旅客,某一天早晨该车从A地出发,晚上到达B地,预定向北为正方向,当天行驶记录如下(单位:千米)
+18,-9,+7,-14,-6,+13,-6,-8
请你根据计算回答下列问题:
(1)B地在A地何方?相距多少千米?
(2)该车这一天共行驶多少千米?
(3)若该车每千米耗油0.4升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于 ![]() EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )
EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( ) 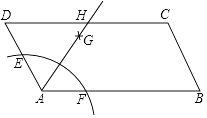
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com