
【题目】图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m). (参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)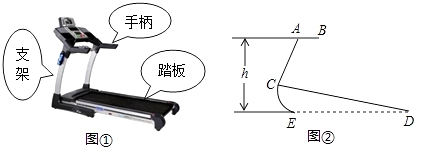
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-![]() x+3
x+3![]() 的图像分别与x轴、y轴交于A、B两点.动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,
的图像分别与x轴、y轴交于A、B两点.动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,![]() ,2 (长度单位/秒);动点E从O点开始以
,2 (长度单位/秒);动点E从O点开始以![]() (长度单位/秒)的速度沿线段OB运动.设P、E两点同时出发,运动时间为t (秒),当点P沿折线AO-OB-BA运动一周时,动点E和P同时停止运动.过点E作EF∥OA,交AB于点F.
(长度单位/秒)的速度沿线段OB运动.设P、E两点同时出发,运动时间为t (秒),当点P沿折线AO-OB-BA运动一周时,动点E和P同时停止运动.过点E作EF∥OA,交AB于点F.
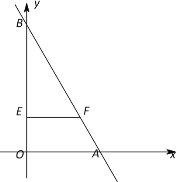
(1)求线段AB的长;
(2)求证:∠ABO=30°;
(3)当t为何值时,点P与点E重合?
(4)当t = 时,PE=PF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.
![]()
(1)写出数轴上点B表示的数;
(2)若点M、N分别是线段AO、BO的中点,求线段MN的长;
(3)若动点P从点A出发.以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.问点P运动多少秒时追上点Q?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点![]() 即各点均表示整数
即各点均表示整数![]() ,且
,且![]() ,若A、D两点表示的数的分别为
,若A、D两点表示的数的分别为![]() 和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是
和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是![]()
![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数 ![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点. 
(1)求一次函数的解析式;
(2)根据图象直接写出 ![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为顺利通过“国家文明城市”验收,东营市政府拟对城区部分路段的人行道地砖、绿化带、排水管道等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com