Question

6．如图，已知∠AOB．请在图中画出∠BOC、射线OM、射线ON，
使得∠AOB＞∠BOC，OM平分∠AOC，ON平分∠BOC．如果
∠AOB=α，∠BOC=β．试用α、β表示∠MON，并说明理由．

Answer 1

分析 由于OA与∠BOC的位置关系不能确定，故应分OA在∠BOC内和在∠BOC外两种情况进行讨论．

解答 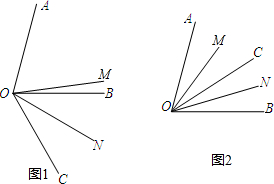解：如图1，∵∠AOB=α，∠BOC=β，
∴∠AOC=α+β，
∵OM平分∠AOC，
∴∠MOC=$\frac{1}{2}$（α+β ），
∵ON平分∠BOC，
∴∠NOC=$\frac{1}{2}$β，
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$α，
如图2，
∵∠AOB=α，∠BOC=β，
∴∠AOC=α-β，
∵OM平分∠AOC，
∴∠MOC=$\frac{1}{2}$（α-β ），
∵ON平分∠BOC，
∴∠NOC=$\frac{1}{2}$β，
∴∠MON=∠MOC+∠NOC=$\frac{1}{2}$α．

点评 本题考查的是角平分线的定义，解答此题时要根据OA与∠BOC的位置关系分两种情况进行讨论，不要漏解．