
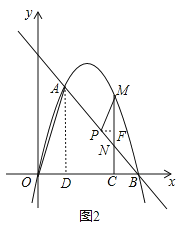
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��l��������![]() �ཻ��A��1��
�ཻ��A��1��![]() ����B��4��0��������
����B��4��0��������
��1����������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D��ʹ�á�ABD�����߶�ABΪб�ߵ�ֱ�������Σ������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�
��3����P���߶�AB��һ���㣬����P�����A��B�غϣ�������P��PM��OA������һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������BCN����PMN�����S��BCN��S��PMN����S��BCN=2S��PMN�����![]() ��ֵ���������ʱ��M��������
��ֵ���������ʱ��M��������
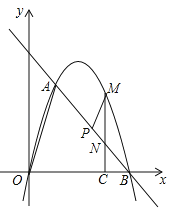
���𰸡���1��![]() ����2��D��1��0������0��
����2��D��1��0������0��![]() ����0��
����0��![]() ������3��
������3��![]() ��M��
��M��![]() ��
��![]() ����
����
��������
�����������1����A��B��������꣬���ô���ϵ��������������߽���ʽ��
��2����D��x���Ϻ�y���ϣ���D��x����ʱ����A��AD��x�ᣬ����D��Ϊ����D����y����ʱ�����D������Ϊ��0��d�����ɷֱ��ʾ��AD��BD�������ù��ɶ����ɵõ�����d�ķ��̣������d��ֵ���Ӷ����������������D�����ꣻ
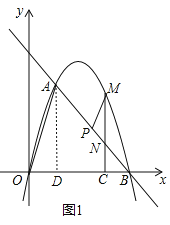
��3����P��PF��CM�ڵ�F������Rt��ADO��Rt��MFP�Լ����Ǻ���������PF�ֱ��ʾ��MF��NF���Ӷ��ɱ�ʾ��MN����BC=a�������a��ʾ��CN��������S��BCN=2S��PMN������PF��ʾ��a��ֵ���Ӷ�����PF��ʾ��CN�������![]() ��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮
��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮
���������
��1����A��1��![]() ����B��4��0����������
����B��4��0����������![]() ��ͼ���ϣ���
��ͼ���ϣ���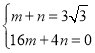 �����
�����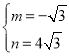 ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2�������������������⣬�������£�
������D��x����ʱ����ͼ1������A��AD��x���ڵ�D����A��1��![]() ������D����Ϊ��1��0����
������D������1��0����
������D��y����ʱ����D��0��d������![]() ��
��![]() ����
����![]() ���ߡ�ABD����ABΪб�ߵ�ֱ�������Σ���
���ߡ�ABD����ABΪб�ߵ�ֱ�������Σ���
![]() ����
����![]() �����d=
�����d=![]() ����D��������0��
����D��������0��![]() ����0��
����0��![]() ����
����
���Ͽ�֪��������������D�㣬������Ϊ��1��0������0��![]() ����0��
����0��![]() ����
����
��3����ͼ2����P��PF��CM�ڵ�F����PM��OA����Rt��ADO��Rt��MFP����![]() =
=![]() ����MF=
����MF=![]() PF����Rt��ABD��BD=3��AD=
PF����Rt��ABD��BD=3��AD=![]() ����tan��ABD=
����tan��ABD=![]() �����ABD=60�㣬��BC=a����CN=
�����ABD=60�㣬��BC=a����CN=![]() a����Rt��PFN�У���PNF=��BNC=30�㣬��tan��PNF=
a����Rt��PFN�У���PNF=��BNC=30�㣬��tan��PNF=![]() ����FN=
����FN=![]() PF����MN=MF+FN=
PF����MN=MF+FN=![]() PF����S��BCN=2S��PMN����
PF����S��BCN=2S��PMN����![]() ����a=
����a=![]() PF����NC=
PF����NC=![]() a=
a=![]() PF����
PF����![]() =
=![]() =
=![]() ����MN=
����MN=![]() NC=
NC=![]() =
=![]() a����MC=MN+NC=��
a����MC=MN+NC=��![]() ��a����M��������4��a����
��a����M������Ϊ��4��a����![]() ��a������M�����������ϣ�����ɵ�
��a������M�����������ϣ�����ɵ�![]() =��
=��![]() ��a�����a=
��a�����a=![]() ��a=0����ȥ����OC=4��a=
��a=0����ȥ����OC=4��a=![]() ��MC=
��MC=![]() �����M��������
�����M��������![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x1��x2��һԪ���η���x2+2x��3=0�Ķ���������x1x2��ֵ�ǣ�������
A.2
B.-2
C.3
D.-3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ�����Ϊ1�������Σ�����һ���������������������Ҽ�����������С�����Σ���ͼ2�����У�����������Χ�ɵ���������ֱ�������Σ��پ���һ�������������ͼ3����������10�κ������������������ȥ��������ø�����֦��Ҷï����
���Ų��ϵ������������γɵ�ͼ�������������ε������Ҳ��֮�仯.������n�κ�ɵ�ͼ�����������ε������Sn��ʾ����ش�
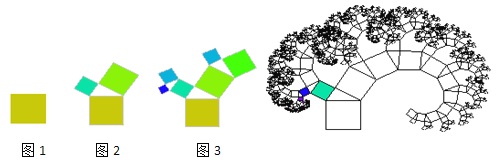
��1��S0�� ��S1�� ��S2�� ��S3�� ��
��2��S0��S1��S2������S10�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η����У���ʵ�����ĺ͵��ک�4���ǣ�������
A.x2+2x��4=0
B.x2��2x+4=0
C.x2��4x��5=0
D.x2+4x��5=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ӽ����IJ��Ͻ�����ʹ�뵼����ϵľ�ϸ�ӹ��ߴ�������С��ij�ֵ���Ԫ���������ԼΪ0.000 000 7ƽ�����ף��ÿ�ѧ��������ʾΪƽ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
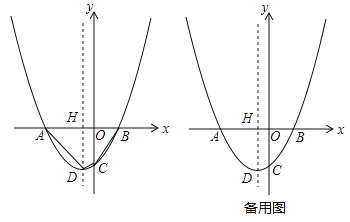
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0��![]() ��������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��l����������P��Q���㣬��Q��y����Ҳ���
��������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��l����������P��Q���㣬��Q��y����Ҳ���
��1����a��ֵ����A��B�����ꣻ
��2����ֱ��l���ı���ABCD��Ϊ�����Ϊ3��7��������ʱ����ֱ��l�ĺ�������ʽ��
��3������Pλ�ڵڶ�����ʱ����PQ���е�ΪM����N���������ϣ�����DPΪ�Խ��ߵ��ı���DMPN�ܷ�Ϊ���Σ����ܣ������N�����ꣻ�����ܣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ƶ��ֻ������ġ����·��������ν��ۣ�ÿ���ۼ���1000Ԫ������810Ԫ����ƽ��ÿ�½��۵İٷ���Ϊ��������
A.9.5%
B.20%
C.10%
D.11%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ʽA=2x2��xy��B=x2+xy��6����
��1��4A��B��
��2����x=1��y=��2ʱ��4A��B��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
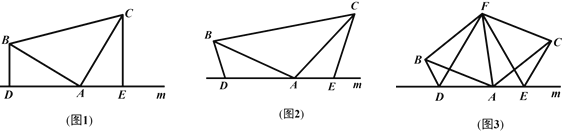
����Ŀ����1����ͼ1����֪������ABC�У���BAC=90�㣬AB=AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E��֤����DE��BD+CE��
��2����ͼ2������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ����ҡ�BDA����AEC����BAC������������Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ�������������������֤����������������˵�����ɣ�
��3����չ��Ӧ�ã���ͼ3��D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E����
�����غϣ�����FΪ��BACƽ�����ϵ�һ�㣬����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE������BDA����AEC����BAC�����ж���DEF����״��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com