

���� ��1�����������֪d=a+8��Ȼ������ʽ���a��ֵ���ٸ�������ȷ����ԭ�㼴�ɣ�
��2���������������������ʱ�䣬�ټ��㼴����⣻
��3������AB=$\frac{2}{3}$AC�г����̣��ٷ�����������ۼ�����⣮
��� �⣺��1����ͼ��֪��d=a+8��
��d-2a=14��
��a+8-2a=14��
���a=-6��
��b=a-2=-8��
��2���ɣ�1����֪��a=-6��b=-8��c=-3��d=2��
��A�˶���D��������ʱ��Ϊ$\frac{8}{3}$��
���˶���ʱ��Ϊt�룬
��A��Ӧ����Ϊ2-3��t-$\frac{8}{3}$��=10-3t��
B��Ӧ����Ϊ��-8+4��t-1��=4t-12��
��A��B��������ʱ��10-3t=4t-12��t=$\frac{22}{7}$��
��4t-12=$\frac{4}{7}$��
��������Ӧ����Ϊ$\frac{4}{7}$��
��3�����˶���ʱ��Ϊt
A��Ӧ����Ϊ��-6-3t
B��Ӧ����Ϊ��-8-4t
��AB=|-6-3t-��-8-4t��|=|t+2|=t+2
��AB=$\frac{2}{3}$AC��
��AC=$\frac{3}{2}$AB=$\frac{3}{2}$t+3��
��C��Ӧ����Ϊ-6��
��AC=|-6-��-6-3t��|=|3t|=$\frac{3}{2}$t+3��
�ٵ�3t=$\frac{3}{2}$t+3��t=2��
�ڵ�3t+$\frac{3}{2}$t+3=0��t=-$\frac{2}{3}$��������ʵ�������
��t=2��
��-6-3t=-12��
�𣺵�A��Ӧ����Ϊ-12
���� ������Ҫ������һԪһ�η��̵�Ӧ���Լ������ϵ������������ʾ������֪ʶ����ȷ��ʾ�����ϵĵ�ľ����ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������֣�
������֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
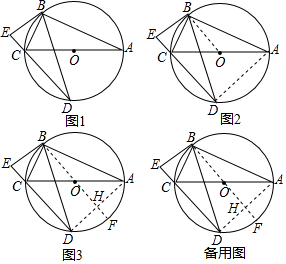
 ��ͼ��CD�ǡ�O��ֱ������A�ǰ�Բ�ϵ����ȷֵ㣬B�ǻ�$\widehat{AD}$���е㣬P��Ϊֱ��CD�ϵ�һ�����㣬��CD=4ʱ��AP+BP����СֵΪ2$\sqrt{2}$��
��ͼ��CD�ǡ�O��ֱ������A�ǰ�Բ�ϵ����ȷֵ㣬B�ǻ�$\widehat{AD}$���е㣬P��Ϊֱ��CD�ϵ�һ�����㣬��CD=4ʱ��AP+BP����СֵΪ2$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
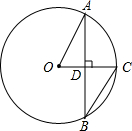 ��ͼ����O����AB��ֱ�뾶OC�ڵ�D����CBA=30�㣬OC=2cm������AB�ij�Ϊ��������
��ͼ����O����AB��ֱ�뾶OC�ڵ�D����CBA=30�㣬OC=2cm������AB�ij�Ϊ��������| A�� | 9cm | B�� | 2$\sqrt{3}$cm | C�� | $\frac{9}{2}$ cm | D�� | $\frac{3\sqrt{3}}{2}$ cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��|a|=-a����a��0 | B�� | ʽ��3xy2-4x3y+12���ߴ�����ʽ | ||
| C�� | ��a��0��ab��0����b��0 | D�� | ��a=b��m������������$\frac{a}{m}$=$\frac{b}{m}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com