
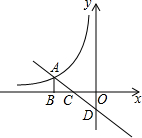
 如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )
如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )| A. | $-\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
分析 设A的横坐标为m,由直线y=kx-1可知C($\frac{1}{k}$,0),根据题意得出$\frac{1}{2}$($\frac{1}{k}$-m)•(-$\frac{6}{m}$)=1,求得km=$\frac{3}{2}$,因为A的纵坐标y=km-1=-$\frac{6}{m}$,进而得出$\frac{3}{2}$-1=-$\frac{6}{m}$,解得m=-12,把m=-12代入km=$\frac{3}{2}$,即可求得k的值.
解答 解:设A的横坐标为m,
由直线y=kx-1可知C($\frac{1}{k}$,0),
∵S△ABC=1,
∴$\frac{1}{2}$($\frac{1}{k}$-m)•(-$\frac{6}{m}$)=1,
解得km=$\frac{3}{2}$,
∵A的纵坐标y=km-1=-$\frac{6}{m}$,
∴$\frac{3}{2}$-1=-$\frac{6}{m}$,
解得m=-12,
∴-12k=$\frac{3}{2}$,
解得k=-$\frac{1}{8}$.
故选A.
点评 本题主要考查反比例函数与一次函数交点问题的知识点,解答本题的关键是进行数形结合进行解题.


科目:初中数学 来源: 题型:选择题
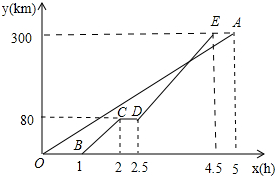 一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法:
一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 1.5 |
| 大于10吨不大于m吨部分(20≤m≤50) | 2 |
| 大于m吨部分 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
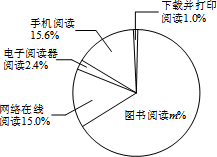 宜兴市2010~2014年成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:
宜兴市2010~2014年成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:| 年份 | 年人均阅读图书数量(本) |
| 2010 | 3.90 |
| 2011 | 4.12 |
| 2012 | 4.35 |
| 2013 | 4.56 |
| 2014 | 4.78 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com