
【题目】计算:(1)(π﹣3)0+![]() ﹣2cos45°﹣
﹣2cos45°﹣![]()
(2)若x+![]() =3,求
=3,求![]() 的值.
的值.
(1)(π﹣3)0+![]() ﹣2cos45°﹣
﹣2cos45°﹣![]()
(2)若x+![]() =3,求
=3,求![]() 的值.
的值.
【答案】
(1)
解:原式=1+3![]() ﹣2×
﹣2×![]() ﹣8=2
﹣8=2![]() ﹣7;
﹣7;
(2)
解:原式=![]()
=![]()
=![]()
=![]() .
.
【解析】(1)根据零指数幂、二次根式的化简、特殊角的三角函数值、负整数指数幂的定义解答;
(2)分子分母同时除以x2 , 配方后整体代入即可解答.
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.
(1)如图1,连接BD,AF,则BD AF(填“>”、“<”或“=”);
(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
(1)(1)求EG:BG的值;
(2)(2)求证:AG=OG;
(3)(3)设AG=a,GH=b,HO=c,求a:b:c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10![]() .四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是 .
.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证: 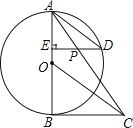
(1)PE=PD
(2)ACPD=APBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.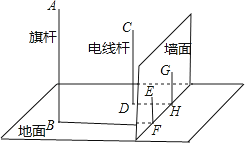
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,n)在抛物线y=x2+bx+c上.
(1)若b=1,c=3,求n的值;
(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是﹣4,请画出点P(x﹣1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com