
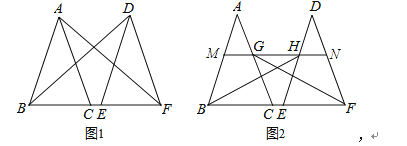
【题目】已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.
(1)如图1,连接BD,AF,则BD AF(填“>”、“<”或“=”);
(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.
【答案】
(1)=
(2)
证明:如图:
MN∥BF,
△AMG∽△ABC,△DHN∽△DEF,
![]() =
=![]() ,
,![]() =
=![]() ,
,
∴MG=HN,MB=NF.
在△BMH和△FNG中,
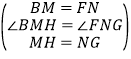 ,
,
△BMH≌△FNG(SAS),
∴BH=FG.
【解析】(1)根据等腰三角形的性质,可得∠ABC与∠ACB的关系,根据平移的性质,可得AC与DF的关系,根据全等三角形的判定与性质,可得答案;
(2)根据相似三角形的判定与性质,可得GM与HN的关系,BM与FN的关系,根据全等三角形的判定与性质,可得答案.
【考点精析】本题主要考查了等腰三角形的性质和平移的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
(1)若AB=4![]() ,求
,求![]() 的长;(结果保留π)
的长;(结果保留π)
(2)求证:四边形ABMC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2 , 再依次连接△A2B2C2的三边中点得△A3B3C3 , …,则△A5B5C5的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1 , 0),B(x2 , 0),与y轴交于点C,且O,C两点间的距离为3,x1x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.
(1)求点C的坐标
(2)当y1随着x的增大而增大时,求自变量x的取值范围;
(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com