
【题目】已知点A(﹣2,n)在抛物线y=x2+bx+c上.
(1)若b=1,c=3,求n的值;
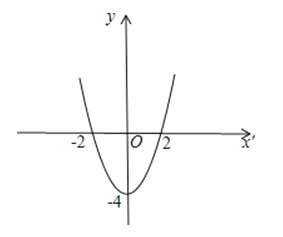
(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是﹣4,请画出点P(x﹣1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.
【答案】
(1)
解:∵b=1,c=3,A(﹣2,n)在抛物线y=x2+bx+c上.
∴n=4+(﹣2)×1+3=5.
(2)
∵此抛物线经过点A(﹣2,n),B(4,n),
∴抛物线的对称轴x=![]() =1,
=1,
∵二次函数y=x2+bx+c的最小值是﹣4,
∴抛物线的解析式为y=(x﹣1)2﹣4,
令x﹣1=x′,
∴点P(x﹣1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x′2﹣4,
点P(x﹣1,x2+bx+c)的纵坐标随横坐标变化的如图:
【解析】(1)代入b=1,c=3,及点A的坐标即可求得n的值;
(2)根据题意求得抛物线的解析式为![]() 从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x'2-4,然后利用五点式画出函数的图象即可.
从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x'2-4,然后利用五点式画出函数的图象即可.
【考点精析】通过灵活运用二次函数的性质和二次函数的最值,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为弘扬“东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
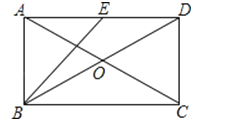
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=![]() ,则BO= ,∠EBD的大小约为 度 分.(参考数据:tan26°34′≈
,则BO= ,∠EBD的大小约为 度 分.(参考数据:tan26°34′≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形网格中,三角形的三个顶点均落在格点上.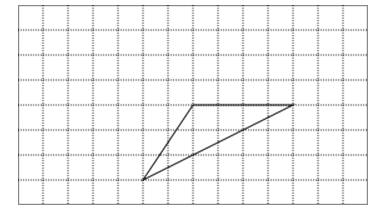
(1)以三角形的其中两边为边画一个平行四边形,并在顶点处标上字母A,B,C,D
(2)证明四边形ABCD是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扑克牌游戏:小明背对小亮,让小亮按下列四个步骤操作:
第一步,分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步,从左边一堆拿出两张,放入中间一堆;
第三步,从右边一堆拿出一张,放入中间一堆;
第四步,左边一堆有几张牌,就从中间一堆拿出几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数,聪明的你,你认为中间一堆牌的张数是多少?
【答案】5
【解析】
此题看似复杂,其实只是考查了整式的基本运算.把每堆牌的数量用相应的字母表示出来,列式表示变化情况即可找出最后答案.
解答:解:设第一步时候,每堆牌的数量都是x(x≥2);
第二步时候:左边x-2,中间x+2,右边x;
第三步时候:左边x-2,中级x+3,右边x-1;
第四步开始时候,左边有(x-2)张牌,则从中间拿走(x-2)张,则中间所剩牌数为(x+3)-(x-2)=x+3-x+2=5.
所以中间一堆牌此时有5张牌.
【题型】填空题
【结束】
44
【题目】为什么总是1 089?
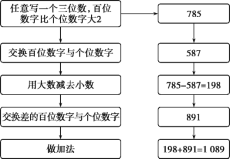
用不同的三位数再试几次,结果都是1 089吗?你能发现其中的原因吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com