
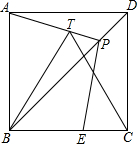
 如图,在正方形ABCD中,E在BC上.
如图,在正方形ABCD中,E在BC上.分析 (1)作PQ⊥AB于Q,作PK⊥BC于K,则四边形BQPK是矩形,得出∠QPK=90°,由正方形的性质得出BD平分∠ABC,得出PQ=PK,由HL证明Rt△APQ≌Rt△EPK,得出∠APQ=∠EPK,由角的互余关系证出∠APE=90°,即可得出结论;
(2)作TH⊥BC于H,则∠THB=∠THC=90°,设BH=x,则CH=15-x,由勾股定理得出方程,解方程求出BH,由勾股定理求出TH,S△TBC=$\frac{1}{2}$BC•TH,即可得出结果.
解答 (1)证明:作PQ⊥AB于Q,作PK⊥BC于K,如图1所示: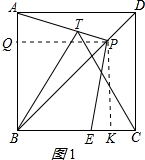 则四边形BQPK是矩形,
则四边形BQPK是矩形,
∴∠QPK=90°,即∠QPE+∠EPK=90°,
∵四边形ABCD是正方形,
∴BD平分∠ABC,
∴PQ=PK,
在Rt△APQ和Rt△EPK中,$\left\{\begin{array}{l}{PA=PE}\\{PQ=PK}\end{array}\right.$,
∴Rt△APQ≌Rt△EPK(HL),
∴∠APQ=∠EPK,
∴∠APQ+∠QPE=90°,
即∠APE=90°,
∴AP⊥PE;
(2)解:作TH⊥BC于H,如图2所示: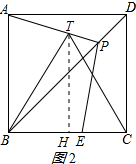 则∠THB=∠THC=90°,
则∠THB=∠THC=90°,
设BH=x,则CH=15-x,
根据勾股定理得:TH2=BT2-BH2,TH2=CT2-CH2,
∴142-x2=132-(15-x)2,
解得:x=$\frac{42}{5}$,
∴TH=$\sqrt{T{B}^{2}-B{H}^{2}}$=$\sqrt{1{4}^{2}-(\frac{42}{5})^{2}}$=$\frac{56}{5}$,
∴S△TBC=$\frac{1}{2}$BC•TH=$\frac{1}{2}$×15×$\frac{56}{5}$=84.
点评 本题考查了正方形的性质、全等三角形的判定与性质、勾股定理、三角形面积的计算;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
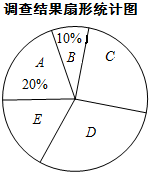 近年来,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
近年来,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.| 组 | 观点 | 人数 |
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 | M |
| C | 汽车尾部排放 | N |
| D | 工厂造成污染 | 120 |
| E | 其他 | 60 |
| A. | 200 | B. | 240 | C. | 440 | D. | 480 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com