
����Ŀ�������������
�����Թ�أ����ܳɷ�Բ�����������ӣ���Բ��һ��ͬ��Ҳ��������ī����
��1��Բ��һ��ͬ��Ҳ���������˹Ŵ����ܶԡ�Բ�������˼���������ִ��ķ��룺____��
������˼����
Բ�������dz��м���ѧϰ���ɻ�ȱ�Ĺ��ߣ���Բ�治�����Ի�Բ�������������Ի����뻡�Ľ��㣬������һ�������Թ���ܶ�ͼ�Σ��磺
��2����ƽ���ߣ���ͼ1��ֻ��Բ���ڡ�AOB�л���һ��Pʹ�õ�P�ڡ�AOB�Ľ�ƽ�����ϣ��ԳƵ㣺��ͼ2��ֻ��Բ��������P����ֱ��l�ĶԳƵ�Q����˵�����ɣ�
 ��������Ӧ�ã�
��������Ӧ�ã�
��3����֪��A��ֱ��l.��ͼ3��ֻ��Բ����ֱ��l�ϻ�������B��C��ʹ��A��B��Cǡ���ǵ��������ε�3�����㣬������һ����д������߶μ��ɣ���
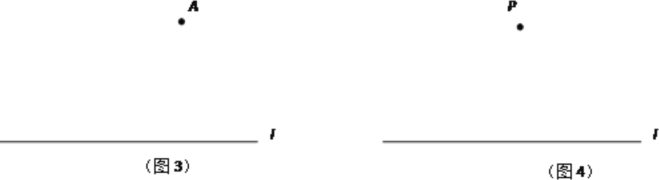
��֪��P��ֱ��l.��ͼ4��ֻ��Բ������һ��Q��ʹ�õ�P��Q���ڵ�ֱ����ֱ��lƽ��.����ʾ��ƽ���ı��ζԱ�ƽ�У���
��4����֪��O��A��B��ֻ��Բ�������뾶ΪAB�ġ�O���A��B����ֱ�ߵĽ���C��D.

���𰸡���1��Բ�ǵ�������ڶ����ĵ�ļ��ϣ���2��ͼ�μ���������3��ͼ�μ���������4��ͼ�μ�����.
��������
��1������Բ�Ķ�����
(2)ͼ1����������ƽ���ߵķ�����ͼ���ɣ�ͼ2�������ζԽ�����ƽ�ִ�ֱ��ͼ���ɽ��
��3���Ե�PΪԲ�ģ����ڵ�P��ֱ��l�ľ��볤Ϊ�뾶��������ֱ��l����B��C���㣬���B��C��Ϊ������ֱ��l����ȡһ��B���Ե�BΪԲ�ģ�PB��Ϊ�뾶��������ֱ��l���ڵ�C�����B��C��Ϊ����
��ֱ��l����ȡB��C���㣬�Ե�PΪԲ�ģ�BC��Ϊ�뾶�������Ե�CΪԲ�ģ�AB��Ϊ�뾶�������������ڵ�Q�����Q��Ϊ����
��4������A��B��ֱ�ߣ��Ե�OΪԲ�ģ�ABΪ�뾶��![]() O,��ֱ��AB�ڵ�C��D.
O,��ֱ��AB�ڵ�C��D.
�⣺(1) Բ�ǵ�������ڶ����ĵ�ļ��ϣ�����������Ҳ���ԣ���
��2����ͼ1�����ɣ���ƽ�����ϵĵ㵽�����ߵľ�����ȡ�

��ͼ2��
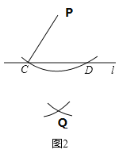
����ͼ2����ֱ��l����ȡ��C��
���Ե�PΪԲ�ģ�PC��Ϊ�뾶��������ֱ��l�ڵ�D��
���ֱ��Ե�C����DΪԲ�ģ�PC��Ϊ�뾶����������ֱ��l������������ΪQ��
���Ե�QΪ����
���ɣ���������ȵ��ı��������Σ����εĶԽ����ഹֱƽ�֣�
(3)����1������һ��
���Ե�PΪԲ�ģ����ڵ�P��ֱ��l�ľ��볤Ϊ�뾶��������ֱ��l����B��C���㣬���B��C��Ϊ����,��ʱPB=PC��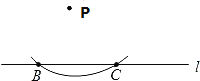
��������
��ֱ��l����ȡһ��B���Ե�BΪԲ�ģ�AB��Ϊ�뾶��������ֱ��l���ڵ�C�����B��C��Ϊ����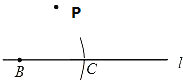
��������
��ֱ��l����ȡB��C���㣬�Ե�PΪԲ�ģ�BC��Ϊ�뾶�������Ե�CΪԲ�ģ�PB��Ϊ�뾶�������������ڵ�Q�����Q��Ϊ����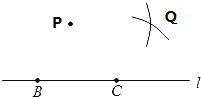
(4)����A��B��ֱ�ߣ��Ե�OΪԲ�ģ�ABΪ�뾶��![]() O,��ֱ��AB�ڵ�C��D.
O,��ֱ��AB�ڵ�C��D.


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD��DE��BC��F����AB���ӳ�����E������EDB=��C.
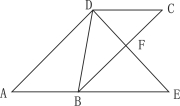
��1����֤����ADE����DBE��
��2����DE=9cm��AE=12cm����DC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
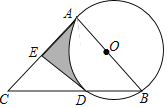
����Ŀ����ͼ��AB�ǡ�O��ֱ����AC�ǡ�O�����ߣ��е�ΪA��BC����O�ڵ�D����E��AC���е㣮
��1�����ж�ֱ��DE���O��λ�ù�ϵ����˵�����ɣ�
��2������O�İ뾶Ϊ2����B=50�㣬AC=4.8����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
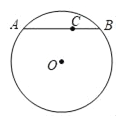
����Ŀ����ͼ��ABΪ��O���ң�CΪ��AB��һ�㣬��AC=m��BC=n��m��n��������AB��Բ��O��תһ�ܣ����߶�BCɨ�������Ϊ��m2��n2���У���![]() =_____��
=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ȫ�������������ǽ�����8�β��ԣ����Գɼ�����λ���������±���
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ���ߴ� | �ڰ˴� | |
�� | 10 | 8 | 9 | 8 | 10 | 9 | 10 | 8 |
�� | 10 | 7 | 10 | 10 | 9 | 8 | 8 | 10 |
��1�����ݱ����е����ݣ��������ƽ���ɼ��� �����ҵ�ƽ���ɼ��� ����
��2���ֱ����ס��������˶�Ա8�β��Գɼ��ķ��
��3�����ݣ�1����2������Ľ��������Ϊ�Ƽ�˭�μ�ȫ�����������ʣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90��AC=BC=1��E��FΪ�߶�AB�������㣬����ECF=45��������E��F�ֱ���BC��AC�Ĵ����ཻ�ڵ�M������ֱ�ΪH��G���������½��ۣ���AB=![]() ��������E���B�غ�ʱ��MH=
��������E���B�غ�ʱ��MH=![]() ����AF+BE=EF����MGMH=
����AF+BE=EF����MGMH=![]() ��������ȷ���۵ĸ����ǣ� ��
��������ȷ���۵ĸ����ǣ� ��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������x�ύ��A��x1��0����B��x2��0�����㣬��x1��x2��y�ύ�ڵ�C��0��4��������x1��x2�Ƿ���x2��4x��12=0����������
��1���������ߵĽ���ʽ��
��2����M���߶�AB�ϵ�һ�����㣬����M��MN��BC����AC�ڵ�N������CM������CMN��������ʱ�����M�����ꣻ
��3����D��4��k���ڣ�1�����������ϣ���EΪ��������һ���㣬��x�����Ƿ���ڵ�F��ʹ��A��D��E��FΪ������ı�����ƽ���ı��Σ�������ڣ�ֱ��д���������������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������ף�ĸ↑��40���������ı�������֪ÿƪ�������ijɼ���m�֣�60��m��100������ί���1000ƪ�����������ȡ�˲��ֲ������ģ�ͳ�������ǵijɼ��������������²�����������ͳ��ͼ����
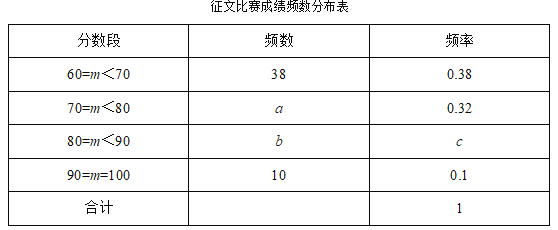
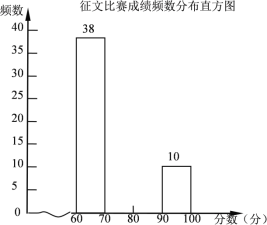
�����������Ϣ������������⣺
��1�����ı����ɼ�Ƶ���ֲ�����c��ֵ��________��
��2����ȫ���ı����ɼ�Ƶ���ֲ�ֱ��ͼ��
��3����80�����ϣ���80�֣������Ľ�����Ϊһ�Ƚ����Թ���ȫ�л��һ�Ƚ����ĵ�ƪ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ű�����ȫ��ͬ��ֽ�ƣ���ͼ��������������������ʾ��������ֱ�д���ĸ���ͬ��������С������4��ֽ�Ʊ��泯��ϴ�Ⱥ���������һ�ţ����Żأ�����������һ�ţ�

��1��д���������Ƴ��ֵ����п��ܵĽ����������������������ʾ����
��2�������������������ϵĽ��Ϊ�����������ж��ı���ABCDΪƽ���ı��εĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com