
ΓΨΧβΡΩΓΩ»γΆΦΘ§±Ώ≥ΛΈΣ4ΒΡ’ΐΖΫ–ΈABCD÷–Θ§ΒψP «±ΏCD…œ“ΜΕ·ΒψΘ§Ής÷±œΏBPΘ§ΙΐAΓΔCΓΔD»ΐΒψΖ÷±πΉς÷±œΏBPΒΡ¥ΙœΏΕΈΘ§¥ΙΉψΖ÷±π «EΓΔFΓΔGΘ°
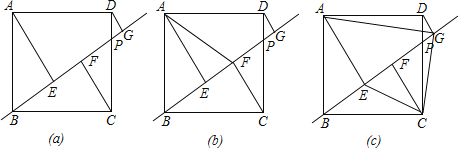
Θ®1Θ©»γΆΦΘ®aΘ©Υυ ΨΘ§Β±CPΘΫ3 ±Θ§«σœΏΕΈEGΒΡ≥ΛΘΜ
Θ®2Θ©»γΆΦΘ®bΘ©Υυ ΨΘ§Β±ΓœPBCΘΫ30Γψ ±Θ§ΥΡ±Ώ–ΈABCFΒΡΟφΜΐΘΜ
Θ®3Θ©»γΆΦΘ®cΘ©Υυ ΨΘ§ΒψP‘ΎCD…œ‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§ΥΡ±Ώ–ΈAECGΒΡΟφΜΐS «Ζώ¥φ‘ΎΉν¥σ÷ΒΘΩ»γΙϊ¥φ‘ΎΘ§«κ«σ≥ωΓœPBCΈΣΕύ…ΌΕ» ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «Εύ…ΌΘΩ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©6+2
ΘΜΘ®2Θ©6+2![]() ΘΜΘ®3Θ©Β±ΓœPBCΈΣ22.5Γψ ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «4+4
ΘΜΘ®3Θ©Β±ΓœPBCΈΣ22.5Γψ ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «4+4![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©―”≥ΛAEΫΜBC”ΎΒψQΘ§ΙΐΒψDΉςDRΓΆAEΘ§”…Χβ“βΩ…÷ΛΥΡ±Ώ–ΈDREG «ΨΊ–ΈΘ§Φ¥DRΘΫEGΘ§”…Ι¥Ι…Ε®άμΩ…«σBPΘΫ5Θ§”…Β»Ϋ«ΒΡ”ύΫ«œύΒ»Ω…ΒΟΓœADRΘΫΓœPBQΘ§Ω…÷ΛΓςADRΓΉΓςPBCΘ§Ω…ΒΟ![]() ,Ω…«σ≥ωDRΘΫ
,Ω…«σ≥ωDRΘΫ![]() Θ§Φ¥EGΘΫ
Θ§Φ¥EGΘΫ![]() ΘΜΘ®2Θ©ΙΐΒψFΉςFMΓΆAB”ΎΒψMΘ§ΉςFNΓΆBC”ΎΒψNΘ§”…Χβ“βΩ…÷ΛΥΡ±Ώ–ΈBNFM «ΨΊ–ΈΘ§Ω…ΒΟFMΘΫBNΘ§”…÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Ω…«σCFΘΫ2Θ§NCΘΫ1Θ§FNΘΫ
ΘΜΘ®2Θ©ΙΐΒψFΉςFMΓΆAB”ΎΒψMΘ§ΉςFNΓΆBC”ΎΒψNΘ§”…Χβ“βΩ…÷ΛΥΡ±Ώ–ΈBNFM «ΨΊ–ΈΘ§Ω…ΒΟFMΘΫBNΘ§”…÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Ω…«σCFΘΫ2Θ§NCΘΫ1Θ§FNΘΫ![]() NCΘΫ
NCΘΫ![]() Θ§Φ¥FMΘΫBNΘΫ3Θ§ΗυΨίSΥΡ±Ώ–ΈABCFΘΫSΓςABF+SΓςBFCΘ§Ω…«σΥΡ±Ώ–ΈABCFΒΡΟφΜΐΘΜΘ®3Θ©Ν§Ϋ”AFΘ§ACΘ§ΙΐΒψDΉςDRΓΆAEΘ§”…ΒΎ“ΜΈ ΒΡΫα¬έΚΆ»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟBFΘΫEGΘ§”…SΥΡ±Ώ–ΈAECGΘΫSΓςAEG+SΓςCEGΘΫ
Θ§Φ¥FMΘΫBNΘΫ3Θ§ΗυΨίSΥΡ±Ώ–ΈABCFΘΫSΓςABF+SΓςBFCΘ§Ω…«σΥΡ±Ώ–ΈABCFΒΡΟφΜΐΘΜΘ®3Θ©Ν§Ϋ”AFΘ§ACΘ§ΙΐΒψDΉςDRΓΆAEΘ§”…ΒΎ“ΜΈ ΒΡΫα¬έΚΆ»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟBFΘΫEGΘ§”…SΥΡ±Ώ–ΈAECGΘΫSΓςAEG+SΓςCEGΘΫ![]() ΓΝEGΓΝAE+
ΓΝEGΓΝAE+![]() ΓΝEGΓΝCFΘΫ
ΓΝEGΓΝCFΘΫ![]() ΓΝBFΓΝAE+
ΓΝBFΓΝAE+![]() ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘΫSΥΡ±Ώ–ΈABCFΘΫSΓςABC+SΓςAFCΘΫ8+SΓςAFCΘ§‘ρΒ±ΒψF‘ΎACΒΡ”“≤ύΘ§«“ΒΫACΨύάκΉν¥σ ±Θ§SΥΡ±Ώ–ΈAECG÷ΒΉν¥σΘ§”…ΒψBΘ§ΒψCΘ§ΒψFΘ§ΒψNΥΡΒψ‘Ύ“‘OΈΣ‘≤–ΡΘ§OCΈΣΑκΨΕΒΡ‘≤…œΘ§Ω…÷ΣΒ±OFΓΆAC ±Θ§ΒψFΒΫACΨύάκΉν¥σΘ§ΗυΨί‘≤ΒΡ”–ΙΊ–‘÷ ΚΆΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Θ§Ω…«σΥΡ±Ώ–ΈAECGΒΡΟφΜΐS «ΒΡΉν¥σ÷ΒΚΆΓœPBCΒΡΕ» ΐΘΜ
ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘΫSΥΡ±Ώ–ΈABCFΘΫSΓςABC+SΓςAFCΘΫ8+SΓςAFCΘ§‘ρΒ±ΒψF‘ΎACΒΡ”“≤ύΘ§«“ΒΫACΨύάκΉν¥σ ±Θ§SΥΡ±Ώ–ΈAECG÷ΒΉν¥σΘ§”…ΒψBΘ§ΒψCΘ§ΒψFΘ§ΒψNΥΡΒψ‘Ύ“‘OΈΣ‘≤–ΡΘ§OCΈΣΑκΨΕΒΡ‘≤…œΘ§Ω…÷ΣΒ±OFΓΆAC ±Θ§ΒψFΒΫACΨύάκΉν¥σΘ§ΗυΨί‘≤ΒΡ”–ΙΊ–‘÷ ΚΆΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Θ§Ω…«σΥΡ±Ώ–ΈAECGΒΡΟφΜΐS «ΒΡΉν¥σ÷ΒΚΆΓœPBCΒΡΕ» ΐΘΜ
ΫβΘΚ
Θ®1Θ©»γΆΦΘ§―”≥ΛAEΫΜBC”ΎΒψQΘ§ΙΐΒψDΉςDRΓΆAEΘ§
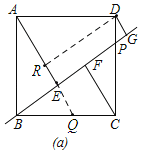
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύADΘΫBCΘΫ4Θ§ADΓΈBCΘ§
ΓύΓœDARΘΫΓœAQBΘ§
ΓΏΓœAQB+ΓœPBCΘΫ90ΓψΘ§ΓœDAR+ΓœADRΘΫ90ΓψΘ§
ΓύΓœADRΘΫΓœPBCΘ§
ΓΏPCΘΫ3Θ§BCΘΫ4Θ§
ΓύBPΘΫ![]() ΘΫ5Θ§
ΘΫ5Θ§
ΓΏΓœADRΘΫΓœPBCΘ§ΓœARDΘΫΓœBCDΘΫ90ΓψΘ§
ΓύΓςADRΓΉΓςPBCΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύDRΘΫ![]() Θ§
Θ§
ÿDRâAEȧDGâBPȧAEâBPȧ
ΓύΥΡ±Ώ–ΈDREG «ΨΊ–ΈΘ§
ΓύEGΘΫDRΘΫ![]() ΘΜ
ΘΜ
Θ®2Θ©»γΆΦΘ§ΙΐΒψFΉςFMΓΆAB”ΎΒψMΘ§ΉςFNΓΆBC”ΎΒψNΘ§
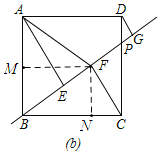
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύABΘΫBCΘΫ4Θ§ΓœABCΘΫ90ΓψΘ§
ΓΏFMΓΆABΘ§FNΓΆBCΘ§ΓœABCΘΫ90ΓψΘ§
ΓύΥΡ±Ώ–ΈBNFM «ΨΊ–ΈΘ§
ΓύFMΘΫBNΘ§
ΓΏΓœPBCΘΫ30ΓψΘ§
ΓύFCΘΫ![]() BCΘΫ2Θ§ΓœFCBΘΫ60ΓψΘ§
BCΘΫ2Θ§ΓœFCBΘΫ60ΓψΘ§
ΓύΓœNFCΘΫ30ΓψΘ§
ΓύNCΘΫ1Θ§FNΘΫ![]() NCΘΫ
NCΘΫ![]() Θ§
Θ§
ΓύBNΘΫBC©¹NCΘΫ4©¹1ΘΫ3ΘΫMFΘ§
ΓύSΥΡ±Ώ–ΈABCFΘΫSΓςABF+SΓςBFCΘ§
ΓύSΥΡ±Ώ–ΈABCFΘΫ![]() ΓΝ4ΓΝ3+
ΓΝ4ΓΝ3+![]() ΓΝ4ΓΝ
ΓΝ4ΓΝ![]() ΘΫ6+2
ΘΫ6+2![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦΘ§Ν§Ϋ”AFΘ§ACΘ§ΙΐΒψDΉςDRΓΆAEΘ§
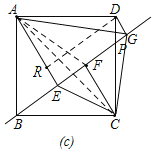
”…ΒΎ“ΜΈ Ω…ΒΟΘ§DRΘΫEGΘ§ΓœADRΘΫΓœPBCΘ§
ΓΏADΘΫBCΘ§ΓœADRΘΫΓœPBCΘ§ΓœARDΘΫΓœCFBΘΫ90ΓψΘ§
ΓύΓςADRΓ’ΓςCBFΘ®AASΘ©
ΓύDRΘΫBFΘ§
ΓύBFΘΫEGΘ§
ΓΏSΥΡ±Ώ–ΈAECGΘΫSΓςAEG+SΓςCEGΘ§
ΓύSΥΡ±Ώ–ΈAECGΘΫ![]() ΓΝEGΓΝAE+
ΓΝEGΓΝAE+![]() ΓΝEGΓΝCFΘΫ
ΓΝEGΓΝCFΘΫ![]() ΓΝBFΓΝAE+
ΓΝBFΓΝAE+![]() ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘ§
ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘ§
ΓύSΥΡ±Ώ–ΈAECGΘΫSΥΡ±Ώ–ΈABCFΘ§
ΓύSΥΡ±Ώ–ΈAECGΘΫSΓςABC+SΓςAFCΘΫ8+SΓςAFCΘ§
ΓύΒ±ΒψF‘ΎACΒΡ”“≤ύΘ§«“ΒΫACΨύάκΉν¥σ ±Θ§SΥΡ±Ώ–ΈAECG÷ΒΉν¥σΘ§
»γΆΦΘ§Ν§Ϋ”BDΫΜAC”ΎΒψNΘ§»ΓBC÷–ΒψOΘ§Ν§Ϋ”ONΘ§OFΫΜAC”ΎΒψMΘ§
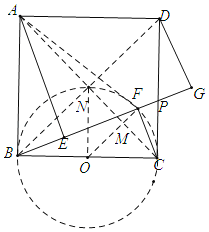
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύΓœBNCΘΫ90ΓψΘΫΓœBFCΘ§BNΘΫCNΘ§
ΓύΒψBΘ§ΒψCΘ§ΒψFΘ§ΒψNΥΡΒψ‘Ύ“‘OΈΣ‘≤–ΡΘ§OCΈΣΑκΨΕΒΡ‘≤…œΘ§
ΓύOCΘΫOFΘΫONΘΫ2Θ§
ΓΏBNΘΫCNΘ§BOΘΫCOΘ§ΓœBNCΘΫ90ΓψΘ§
ΓύΓœCONΘΫ90ΓψΘ§ΓœBCNΘΫΓœCNOΘΫ45ΓψΘ§
ΓύNCΘΫ![]() Θ§
Θ§
Φ¥ACΘΫ![]() Θ§
Θ§
Β±OFΓΆAC ±Θ§ΒψFΒΫACΒΡΨύάκΉν¥σΘ§
ΓΏOFΓΆACΘ§ONΘΫOCΘ§ΓœNOCΘΫ90ΓψΘ§
ΓύOMΘΫMNΘΫMCΘΫ![]() Θ§ΓœFOCΘΫΓœNOCΘΫ45ΓψΘ§
Θ§ΓœFOCΘΫΓœNOCΘΫ45ΓψΘ§
ΓύFMΘΫ2©¹![]() Θ§
Θ§
ΓύΥΡ±Ώ–ΈAECGΒΡΟφΜΐSΒΡΉν¥σ÷ΒΘΫ8+![]() ΓΝ4
ΓΝ4![]() ΓΝΘ®2©¹
ΓΝΘ®2©¹![]() Θ©ΘΫ4+4
Θ©ΘΫ4+4![]() Θ§
Θ§
ΓΏOBΘΫOFΘ§
ΓύΓœPBOΘΫΓœOFBΘ§
ΓΏΓœPBO+ΓœOFBΘΫΓœFOCΘΫ45ΓψΘ§
ΓύΓœPBCΘΫ22.5ΓψΘ§
ΓύΒ±ΓœPBCΈΣ22.5Γψ ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «4+4![]() .
.


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
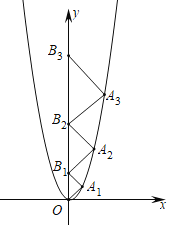
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐyΘΫ2x2ΒΡΆΦœσ»γΆΦΥυ ΨΘ§Ήχ±ξ‘≠ΒψOΘ§ΒψB1Θ§B2Θ§B3‘Ύy÷αΒΡ’ΐΑκ÷α…œΘ§ΒψA1Θ§A2Θ§A3‘ΎΕΰ¥ΈΚ· ΐyΘΫ2x2ΈΜ”ΎΒΎ“ΜœσœόΒΡΆΦœσ…œΘ§»τΓςA1OB1Θ§ΓςA2B1B2Θ§ΓςA3B2B3ΕΦΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“ΒψA1Θ§A2Θ§A3ΨυΈΣ÷±Ϋ«ΕΞΒψΘ§‘ρΒψA3ΒΡΉχ±ξ «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ΫΪΓςABC»ΤΕΞΒψCΡφ ±’κ–ΐΉΣΒΟΒΫΓςAΓδBΓδCΘ§M «BCΒΡ÷–ΒψΘ§P «AΓδBΓδΒΡ÷–ΒψΘ§Ν§Ϋ”PMΘ§»τBCΘΫ2Θ§ΓœBACΘΫ30ΓψΘ§‘ρœΏΕΈPMΒΡΉν¥σ÷Β «_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
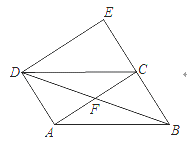
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABCD÷–Θ§ΒψE‘ΎBC―”≥ΛœΏ…œΘ§ECΘΫBCΘ§Ν§Ϋ”DEΘ§ACΘ§ACΓΆAD”ΎΒψAΓΔ
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈACED «ΨΊ–ΈΘΜ
Θ®2Θ©Ν§Ϋ”BDΘ§ΫΜAC”ΎΒψFΘ°»τACΘΫ2ADΘ§≤¬œκΓœE”κΓœBDEΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡ≤¬œκΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΟύ―τΡ≥ΙΪΥΨœζ έΆ≥ΦΤΝΥΟΩΗωœζ έ‘±‘ΎΡ≥‘¬ΒΡœζ έΕνΘ§Μφ÷ΤΝΥ»γœ¬’έœΏΆ≥ΦΤΆΦΚΆ…»–ΈΆ≥ΦΤΆΦΘΚ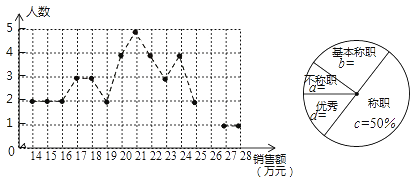
…ηœζ έ‘±ΒΡ‘¬œζ έΕνΈΣxΘ®ΒΞΈΜΘΚΆρ‘ΣΘ©ΓΘœζ έ≤ΩΙφΕ®ΘΚΒ±x<16 ±Θ§ΈΣΓΑ≤Μ≥Τ÷ΑΓ±Θ§Β± ![]() ±ΈΣΓΑΜυ±Ψ≥Τ÷ΑΓ±Θ§Β±
±ΈΣΓΑΜυ±Ψ≥Τ÷ΑΓ±Θ§Β±![]() ±ΈΣΓΑ≥Τ÷ΑΓ±Θ§Β±
±ΈΣΓΑ≥Τ÷ΑΓ±Θ§Β±![]() ±ΈΣΓΑ”≈–ψΓ±.ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
±ΈΣΓΑ”≈–ψΓ±.ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©≤Ι»Ϊ’έœΏΆ≥ΦΤΆΦΚΆ…»–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©«σΥυ”–ΓΑ≥Τ÷ΑΓ±ΚΆΓΑ”≈–ψΓ±ΒΡœζ έ‘±œζ έΕνΒΡ÷–ΈΜ ΐΚΆ÷Ύ ΐΘΜ
Θ®3Θ©ΈΣΝΥΒςΕ·œζ έ‘±ΒΡΜΐΦΪ–‘Θ§œζ έ≤ΩΨωΕ®÷ΤΕ®“ΜΗω‘¬œζ έΕνΫ±άχ±ξΉΦΘ§Ζ≤‘¬œζ έΕν¥οΒΫΜρ≥§Ιΐ’βΗω±ξΉΦΒΡœζ έ‘±ΫΪΜώΒΟΫ±άχΓΘ»γΙϊ“Σ ΙΒΟΥυ”–ΓΑ≥Τ÷ΑΓ±ΚΆΓΑ”≈–ψΓ±ΒΡœζ έ‘±ΒΡ“ΜΑκ»Υ‘±ΡήΜώΫ±Θ§‘¬œζ έΕνΫ±άχ±ξΉΦ”ΠΕ®ΈΣΕύ…ΌΆρ‘ΣΘ®ΫαΙϊ»Ξ’ϊ ΐΘ©ΘΩ≤ΔΦρ ωΤδάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―τΙβ –≥ΓΡ≥ΗωΧε…ΧΜßΙΚΫχΡ≥÷÷ΒγΉ”≤ζΤΖΘ§ΟΩΗωΫχΦέ50‘ΣΘ°Βς≤ιΖΔœ÷Θ§Β± έΦέΈΣ80‘Σ ±Θ§ΤΫΨυ“Μ÷ήΩ…¬τ≥ω160ΗωΘ§ΕχΒ±ΟΩ έΦέΟΩΫΒΒΆ2‘Σ ±Θ§ΤΫΨυ“Μ÷ήΩ…Εύ¬τ≥ω20ΗωΘ°»τ…ηΟΩΗωΒγΉ”≤ζΤΖΫΒΦέx‘ΣΘ§
Θ®1Θ©ΗυΨίΧβ“βΘ§Χν±μΘΚ
ΫχΦέΘ®‘ΣΘ© | έΦέΘ®‘ΣΘ© | ΟΩΦΰάϊ»σΘ®‘ΣΘ© | œζΝΩΘ®ΗωΘ© | Ήήάϊ»σΘ®‘ΣΘ© | |
ΫΒΦέ«Α | 50 | 80 | 30 | 160 |
|
ΫΒΦέΚσ | 50 | ________ | ________ | ________ | ________ |
Θ®2Θ©»τ…ΧΜßΦΤΜ°ΟΩ÷ή”·άϊ5200‘ΣΘ§«“ΨΓΝΩΦθ…ΌΩβ¥φΘ§‘ρΟΩΗωΒγΉ”≤ζΤΖ”ΠΫΒΦέΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
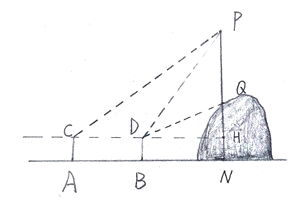
ΓΨΧβΡΩΓΩ–ΓΟς―ß–ΘΟ≈«Α”–Ήυ…ΫΘ§…Ϋ…œ”–“ΜΒγœΏΗΥPQΘ§ΥϊΚήœκ÷ΣΒάΒγœΏΗΥPQ ΒΡΗΏΕ».”Ύ «Θ§”–“ΜΧλΘ§–ΓΟςΚΆΥϊΒΡΆ§―ß–ΓΝΝ¥χΉ≈≤ύ«ψΤςΚΆΤΛ≥Ώά¥ΒΫ…ΫΫ≈œ¬Ϋχ––≤βΝΩ.≤βΝΩΖΫΑΗ»γœ¬ΘΚ»γΆΦΘ§ Ήœ»Θ§–ΓΟς’Ψ‘ΎΒΊΟφ…œΒΡΒψA¥ΠΘ§≤βΒΟΒγœΏΗΥΕΞΕΥΒψPΒΡ―ωΫ« «45![]() ΘΜ»ΜΚσ–ΓΟςœρ«ΑΉΏ6ΟΉΒΫ¥οΒψB¥ΠΘ§≤βΒΟΒγœΏΗΥΕΞΕΥΒψPΚΆΒγœΏΗΥΒΉΕΥΒψQΒΡ―ωΫ«Ζ÷±π «60
ΘΜ»ΜΚσ–ΓΟςœρ«ΑΉΏ6ΟΉΒΫ¥οΒψB¥ΠΘ§≤βΒΟΒγœΏΗΥΕΞΕΥΒψPΚΆΒγœΏΗΥΒΉΕΥΒψQΒΡ―ωΫ«Ζ÷±π «60![]() ΚΆ30
ΚΆ30![]() Θ§…η–ΓΟςΒΡ―έΨΠΒΫΒΊΟφΒΡΨύάκΈΣ1.6ΟΉ.«κΗυΨί“‘…œ≤βΝΩΒΡ ΐΨίΘ§ΦΤΥψΒγœΏΗΥPQΒΡΗΏΕ»Θ®ΫαΙϊΨΪ»ΖΒΫ1ΟΉΘ©≤ΈΩΦ ΐΨίΘΚ
Θ§…η–ΓΟςΒΡ―έΨΠΒΫΒΊΟφΒΡΨύάκΈΣ1.6ΟΉ.«κΗυΨί“‘…œ≤βΝΩΒΡ ΐΨίΘ§ΦΤΥψΒγœΏΗΥPQΒΡΗΏΕ»Θ®ΫαΙϊΨΪ»ΖΒΫ1ΟΉΘ©≤ΈΩΦ ΐΨίΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΈΣΓ―OΒΡ÷±ΨΕΘ§PD«–Γ―O”ΎΒψCΘ§”κBAΒΡ―”≥ΛœΏΫΜ”ΎΒψDΘ§DEΓΆPOΫΜPO―”≥ΛœΏ”ΎΒψEΘ§Ν§Ϋ”PBΘ§ΓœEDB=ΓœEPBΘ°
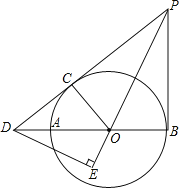
Θ®1Θ©«σ÷ΛΘΚPB «ΒΡ«–œΏΘ°
Θ®2Θ©»τPB=6Θ§DB=8Θ§«σΓ―OΒΡΑκΨΕΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ νΦΌ «¬Ο”ΈΆζΦΨΘ§ΈΣΈϋ“ΐ”ΈΩΆΘ§Ρ≥¬Ο”ΈΙΪΥΨΆΤ≥ωΝΫΧθΓΑΨΪΤΖ¬ΖœΏΓ±ΓΣΓΣΓΑ«ΉΉ””ΈΓ±ΚΆΓΑœΡΝν”ΣΓ±ΓΘΘ®1Θ©7‘¬ΖίΘ§ΓΑ«ΉΉ””ΈΓ±ΚΆΓΑœΡΝν”ΣΓ±ΜνΕ·ΒΡΦέΗώΖ÷±πΈΣ8000‘Σ/»ΥΚΆ12000‘Σ/»ΥΓΘΤδ÷–Θ§≤ΈΦ”ΓΑœΡΝν”ΣΓ±ΜνΕ·ΒΡ”ΈΩΆ»Υ ΐΈΣΓΑ«ΉΉ””ΈΓ±ΜνΕ·”ΈΩΆ»Υ ΐΒΡ2±Ε…Ό300»ΥΘ§«“ΓΑœΡΝν”ΣΓ±œΏ¬ΖΒΡ¬Ο”ΈΉή ’»κ≤ΜΒΆ”ΎΓΑ«ΉΉ””ΈΓ±œΏ¬Ζ¬Ο”ΈΉή ’»κΒΡ“ΜΑκΘ§
Έ ΘΚΘ®1Θ©≤ΈΦ”ΓΑ«ΉΉ””ΈΓ±œΏ¬ΖΒΡ¬Ο”Έ»Υ ΐ÷Ν…Ό”–Εύ…Ό»ΥΘΩ
Θ®2Θ©ΒΫΝΥ8‘¬ΖίΘ§ΗϬϔΈΙΪΥΨ Β––ΫΒΦέ¥ΌœζΜνΕ·Θ§ΓΑ«ΉΉ””ΈΓ±ΚΆΓΑœΡΝν”ΣΓ±œΏ¬ΖΒΡΦέΗώΖ÷±πœ¬ΫΒ![]() ΚΆ
ΚΆ![]() (
(![]() <20)Θ§¬Ο”Έ»Υ ΐ‘Ύ7‘¬ΖίΕ‘”ΠΉν–Γ÷ΒΒΡΜυ¥Γ…œΖ÷±π…œ…ΐ
<20)Θ§¬Ο”Έ»Υ ΐ‘Ύ7‘¬ΖίΕ‘”ΠΉν–Γ÷ΒΒΡΜυ¥Γ…œΖ÷±π…œ…ΐ![]() ΚΆ
ΚΆ![]() ,Β±‘¬¬Ο”ΈΉή ’»κ¥οΒΫ256.32Άρ‘ΣΘ§«σ
,Β±‘¬¬Ο”ΈΉή ’»κ¥οΒΫ256.32Άρ‘ΣΘ§«σ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com