
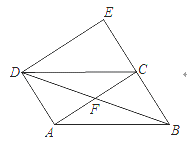
【题目】如图,ABCD中,点E在BC延长线上,EC=BC,连接DE,AC,AC⊥AD于点A、
(1)求证:四边形ACED是矩形;
(2)连接BD,交AC于点F.若AC=2AD,猜想∠E与∠BDE的数量关系,并证明你的猜想.
【答案】(1)证明见解析(2)∠E=2∠BDE
【解析】
(1)由四边形ABCD是平行四边形,EC=BC,易证得四边形ACED是平行四边形,又由AC⊥AD,即可证得四边形ACED是矩形;
(2)根据矩形的性质得∠E=∠DAC=90°,可证得DA=AF,由等腰三角形的性质可得∠ADF=45°,则∠BDE=45°,可得出∠E=2∠BDE.
(1)证明:因为ABCD是平行边形,
∴AD=BC,AD∥BC,
∵BC=CE,点E在BC的延长线上,
∴AD=EC,AD∥EC,
∴四边形ACED为平行四边形,
∵AC⊥AD,
∴平行四边形ACED为矩形
(2)∠E=2∠BDE
理由:∵平行四边形ABCD中,AC=2AF,
又∵AC=2AD,
∴AD=AF,
∴∠ADF=∠AFD,
∵AC∥ED,
∴∠BDE=∠BFC,
∵∠BFC=∠AFD,
∴∠BDE=∠ADF=45°,
∴∠E=2∠BDE


科目:初中数学 来源: 题型:
【题目】某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如表:
原科维生素C及价格 | 甲种原料 | 乙种原料 |
维生素c(单位/千克) | 600 | 400 |
原料价格(元/千克) | 9 | 5 |
现要配制这种营养食品20千克,设购买甲种原料x千克,购买这两种原料的总费用为y元.
(1)求y与x的函数关系式?
(2)若食堂要求营养食品每千克至少含有480单位的维生素C,试说明需要购买甲种原料多少千克时,总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为决定谁获得仅有的一张电影票,甲和乙设计了如下游戏:在三张完全相同的卡片上,分别写上字母![]() ,
,![]() ,
,![]() ,背面朝上,每次活动洗均匀.
,背面朝上,每次活动洗均匀.
甲说:我随机抽取一张,若抽到字母![]() ,电影票归我;
,电影票归我;
乙说:我随机抽取一张后放回,再随机抽取一张,若两次抽取的字母相同的电影票归我.
![]() 求甲获得电影票的概率;
求甲获得电影票的概率;![]() 求乙获得电影票的概率;
求乙获得电影票的概率;![]() 此游戏对谁有利?
此游戏对谁有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (m为常数).
(m为常数).
(1)试判断该函数的图象与x轴的公共点的个数;
(2)求证:不论m为何值,该函数的图象的顶点都在函数![]() 的图象上;
的图象上;
(3)若直线y=x与二次函数图象交于A、B两点,当﹣4≤m≤2时,求线段AB的最大值和最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
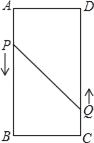
【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?
(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
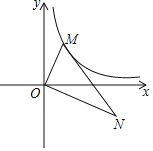
【题目】如图,在平面直角坐标系中,点M、N分别为反比例函数y=![]() 和y=
和y=![]() 的图象上的点,顺次连接M、O、N,∠MON=90°,∠ONM=30°,则k=_____.
的图象上的点,顺次连接M、O、N,∠MON=90°,∠ONM=30°,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD中,点P是边CD上一动点,作直线BP,过A、C、D三点分别作直线BP的垂线段,垂足分别是E、F、G.
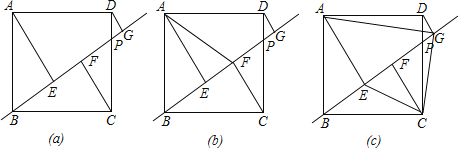
(1)如图(a)所示,当CP=3时,求线段EG的长;
(2)如图(b)所示,当∠PBC=30°时,四边形ABCF的面积;
(3)如图(c)所示,点P在CD上运动的过程中,四边形AECG的面积S是否存在最大值?如果存在,请求出∠PBC为多少度时,S有最大值,最大值是多少?如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
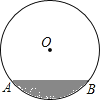
【题目】在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.
(1)若油面宽AB=16dm,求油的最大深度.
(2)在(1)的条件下,若油面宽变为CD=30dm,求油的最大深度上升了多少dm?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com