
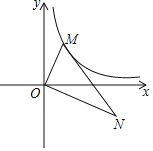
【题目】如图,在平面直角坐标系中,点M、N分别为反比例函数y=![]() 和y=
和y=![]() 的图象上的点,顺次连接M、O、N,∠MON=90°,∠ONM=30°,则k=_____.
的图象上的点,顺次连接M、O、N,∠MON=90°,∠ONM=30°,则k=_____.
科目:初中数学 来源: 题型:
【题目】如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是( )
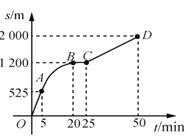
A.25min~50min,王阿姨步行的路程为800m
B.线段CD的函数解析式为![]()
C.5min~20min,王阿姨步行速度由慢到快
D.曲线段AB的函数解析式为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
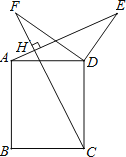
【题目】如图,四边形ABCD是矩形,点E、F是矩形ABCD外两点,AE⊥CF于H,AD=3,DC=4,DE=![]() ,∠EDF=90°,则DF的长是( )
,∠EDF=90°,则DF的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
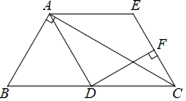
【题目】如图,在△ABC中,∠BAC=90°,点D是BC中点,AE∥BC,CE∥AD.
(1)求证:四边形ADCE是菱形;
(2)过点D作DF⊥CE于点F,∠B=60°,AB=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
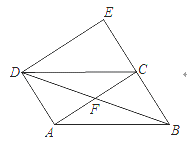
【题目】如图,ABCD中,点E在BC延长线上,EC=BC,连接DE,AC,AC⊥AD于点A、
(1)求证:四边形ACED是矩形;
(2)连接BD,交AC于点F.若AC=2AD,猜想∠E与∠BDE的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作☉O,交BD于点E,连接CE,过D作DF![]() AB于点F,∠BCD=2∠ABD.
AB于点F,∠BCD=2∠ABD.
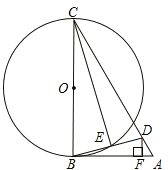
(1)求证:AB是☉O的切线;
(2)若∠A=60°,DF=![]() ,求☉O的直径BC的长。
,求☉O的直径BC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光市场某个体商户购进某种电子产品,每个进价50元.调查发现,当售价为80元时,平均一周可卖出160个,而当每售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,
(1)根据题意,填表:
进价(元) | 售价(元) | 每件利润(元) | 销量(个) | 总利润(元) | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 | ________ | ________ | ________ | ________ |
(2)若商户计划每周盈利5200元,且尽量减少库存,则每个电子产品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=6.点P在边AC上运动,过点P作PD⊥AB于点D,以AP、AD为邻边作PADE.设□PADE与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x≤6).
(1)求线段PE的长(用含x的代数式表示).
(2)当点E落在边BC上时,求x的值.
(3)求y与x之间的函数关系式.
(4)直接写出点E到△ABC任意两边所在直线距离相等时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“书”、“香”、“校”、“园”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是“书”的概率为多少?
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“书香”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com