
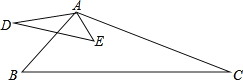
【题目】如图,若![]() ,添加一个条件使
,添加一个条件使![]() ,则添加的条件是________.
,则添加的条件是________.
【答案】![]() 或者∠DAB=∠CAE,∠DAE=∠BAC.
或者∠DAB=∠CAE,∠DAE=∠BAC.
【解析】
由已知及相似三角形的判定可以从边和角两方面考虑解答.(1)由边解答,已知两组对应边成比例,只要添加第三组对应边成比例即可.(2)由角解答,只要添加已知两组对应边的夹角∠DAB和∠BAC相等即可,又由∠DAB=∠CAE也能推出∠DAB和∠BAC相等即△ADE∽△ACB.
由已知,
若![]() ,则△ADE∽△ACB.
,则△ADE∽△ACB.
若![]() ,∠DAE=∠BAC,则△ADE∽△ACB.
,∠DAE=∠BAC,则△ADE∽△ACB.
若∠DAB=∠CAE,则∠DAB+∠BAE=∠CAE+∠BAE,即,∠DAE=∠BAC,又![]() ,则△ADE∽△ACB.
,则△ADE∽△ACB.
故答案为:![]() 或者∠DAB=∠CAE,∠DAE=∠BAC.
或者∠DAB=∠CAE,∠DAE=∠BAC.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段![]() (点A,B的对应点分别为
(点A,B的对应点分别为![]() ).画出线段
).画出线段![]() ;
;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() .画出线段
.画出线段![]() ;
;
(3)以![]() 为顶点的四边形
为顶点的四边形![]() 的面积是 个平方单位.
的面积是 个平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
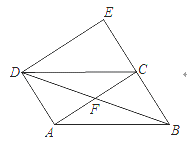
【题目】如图,ABCD中,点E在BC延长线上,EC=BC,连接DE,AC,AC⊥AD于点A、
(1)求证:四边形ACED是矩形;
(2)连接BD,交AC于点F.若AC=2AD,猜想∠E与∠BDE的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光市场某个体商户购进某种电子产品,每个进价50元.调查发现,当售价为80元时,平均一周可卖出160个,而当每售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,
(1)根据题意,填表:
进价(元) | 售价(元) | 每件利润(元) | 销量(个) | 总利润(元) | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 | ________ | ________ | ________ | ________ |
(2)若商户计划每周盈利5200元,且尽量减少库存,则每个电子产品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
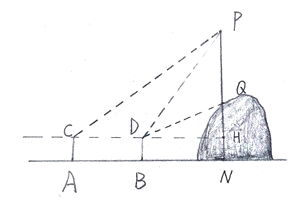
【题目】小明学校门前有座山,山上有一电线杆PQ,他很想知道电线杆PQ 的高度.于是,有一天,小明和他的同学小亮带着侧倾器和皮尺来到山脚下进行测量.测量方案如下:如图,首先,小明站在地面上的点A处,测得电线杆顶端点P的仰角是45![]() ;然后小明向前走6米到达点B处,测得电线杆顶端点P和电线杆底端点Q的仰角分别是60
;然后小明向前走6米到达点B处,测得电线杆顶端点P和电线杆底端点Q的仰角分别是60![]() 和30
和30![]() ,设小明的眼睛到地面的距离为1.6米.请根据以上测量的数据,计算电线杆PQ的高度(结果精确到1米)参考数据:
,设小明的眼睛到地面的距离为1.6米.请根据以上测量的数据,计算电线杆PQ的高度(结果精确到1米)参考数据:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=6.点P在边AC上运动,过点P作PD⊥AB于点D,以AP、AD为邻边作PADE.设□PADE与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x≤6).
(1)求线段PE的长(用含x的代数式表示).
(2)当点E落在边BC上时,求x的值.
(3)求y与x之间的函数关系式.
(4)直接写出点E到△ABC任意两边所在直线距离相等时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
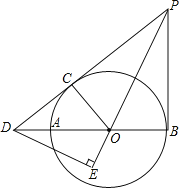
(1)求证:PB是的切线.
(2)若PB=6,DB=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com