
 ,∠DPA=45°.
,∠DPA=45°.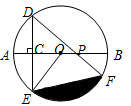
 .
. AO=
AO= OE,解直角三角形求解.
OE,解直角三角形求解. DE=
DE= .∵DE平分AO,∴CO=
.∵DE平分AO,∴CO= AO=
AO= OE.又∵∠OCE=90°,∴sin∠CEO=
OE.又∵∠OCE=90°,∴sin∠CEO= =
= ,∴∠CEO=30°.在Rt△COE中,OE=
,∴∠CEO=30°.在Rt△COE中,OE= =
= .∴⊙O的半径为2.
.∴⊙O的半径为2. .∵∠EOF=2∠D=90°,OE=OF=2,∴SRt△OEF=
.∵∠EOF=2∠D=90°,OE=OF=2,∴SRt△OEF= ×OE×OF=2.∴S阴影=S扇形OEF﹣SRt△OEF=
×OE×OF=2.∴S阴影=S扇形OEF﹣SRt△OEF= .
.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
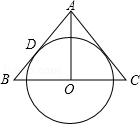
 的灰色扇形OAB,其中OA的长度 为6
的灰色扇形OAB,其中OA的长度 为6  ,且OA与地面垂直.若在没有滑动的情况下,将图(甲)的扇形向右滚动至点A再一次接触地面,如图(乙)所示,则O点移动了( )
,且OA与地面垂直.若在没有滑动的情况下,将图(甲)的扇形向右滚动至点A再一次接触地面,如图(乙)所示,则O点移动了( )

| A.11p | B.12p | C.10p +  | D.11p + |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com