
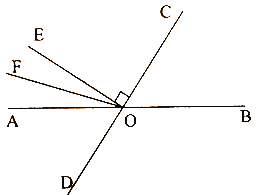
【题目】已知:如图,直线AB、CD相交于点O,OE⊥OC,OF平分∠AOE.
(1)若![]() ,则∠AOF的度数为______;
,则∠AOF的度数为______;
(2)若![]() ,求∠BOC的度数。
,求∠BOC的度数。
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据对顶角的性质得到∠AOD=∠BOC=60°,根据垂直的定义得到∠DOE=90°,根据角平分线的定义即可得到结论;
(2)由垂直的定义得到∠DOE=∠COE=90°,根据角平分线的定义得到∠AOE=2∠EOF=180°-2x°,根据对顶角的性质即可得到结论.
∵∠AOD=∠BOC=60°,
∵OE⊥OC于点O,
∴∠DOE=90°,
∴∠AOE=30°,
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=15°,
∠AOE=15°,
故答案为:15°;
(2)∵OE⊥OC于点O,
∴∠COE=∠DOE=90°,
∵∠COF=x°,
∴∠EOF=x°90°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=2x°180°,
∴∠AOD=90°∠AOE=270°2x°,
∴∠BOC=∠AOD=270°2x°.
故答案为:270°2x°.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
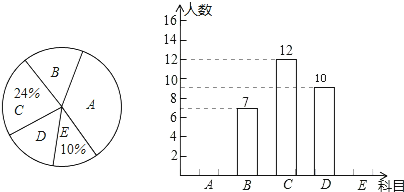
A.选科目E的有5人
B.选科目D的扇形圆心角是72°
C.选科目A的人数占体育社团人数的一半
D.选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重合的四边形EFGH,EH=12cm,EF=l6cm则边AD的长是( )
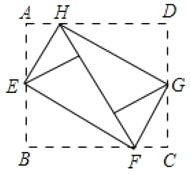
A.12cmB.16cmC.20cmD.24cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:某数学兴趣小组把两个等腰直角三角形的直角顶点重合,发现了一些有趣的结论.
结论一:
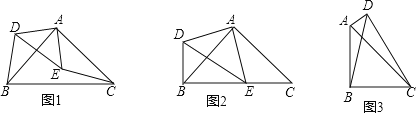
(1)如图1,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BD,CE,试说明△ADB≌△AEC;
结论二:
(2)如图2,在(1)的条件下,若点E在BC边上,试说明DB⊥BC;
应用:
(3)如图3,在四边形ABCD中,∠ABC=∠ADC=90°,AB=CB,∠BAD+∠BCD=180°,连接BD,BD=7cm,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.
(1)线段AC的长=________;
(2)当△PCF与△EDF相似时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),则点A,B的对应点A1,B1的坐标分别为 ;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为![]() 、
、![]() ,
,![]() ,若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A′B′C′,点A、B、C的对应点分别为A′、B′、C′。
,若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A′B′C′,点A、B、C的对应点分别为A′、B′、C′。
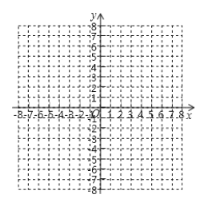
(1)写出点A′、B′、C′的坐标;
(2)在图中画出平移后的三角形A′B′C′;
(3)三角形A′B′C′的面积为_____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com