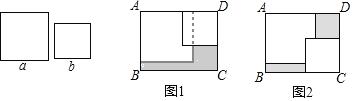
【题目】在长方形
内，若两张边长分别为
和
（
）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），长方形总未被这两张正方形纸片覆盖的部分用阴影表示，若图1中阴影部分的面积为
，图2中阴影部分的面积和为
，则关于，的大小关系表述正确的是（ ）
A.
B.
C.
D.无法确定
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知BE平分∠ABD，DE平分∠BDC，且∠BED =∠ABE +∠EDC．
（1）如图1，求证：AB//CD；
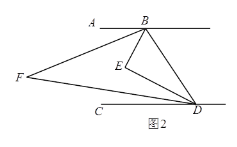
（2）如图2，若∠ABE=3∠ABF，且∠BFD=30°时，试求
的值；
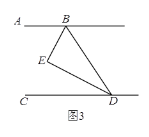
（3）如图3，若H是直线CD上一动点（不与D重合），BI平分∠HBD，画出图形，并探究出∠EBI与∠BHD的数量关系．
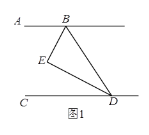
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．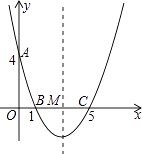
（1）求抛物线的解析式和对称轴；
（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
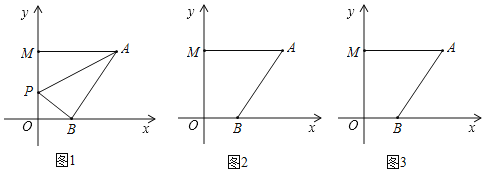
【题目】在平面直角坐标系中，A(6，a)，B(b，0)，M(0，c)，P点为y轴上一动点，且(b﹣2)2+|a﹣6|+
＝0．
(1)求点B、M的坐标；
(2)当P点在线段OM上运动时，试问是否存在一个点P使S△PAB＝13，若存在，请求出P点的坐标与AB的长度；若不存在，请说明理由．
(3)不论P点运动到直线OM上的任何位置(不包括点O、M)，∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系，如果有，请利用所学知识找出并证明；如果没有，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】荣荣是个爱动脑筋的同学，在发现教材中的用方框在月历中移动的规律后，突发奇想，将连续的偶数2、4、6、8，…排成如下表,并用一个十字形框架住其中的五个数,请你仔细观察十字形框架中数字的规律,并回答下列问题:
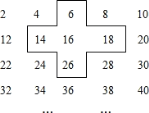
十字框中的五个数的和与中间的数16有什么关系?
设中间的数为x，用代数式表示十字框中的五个数的和；
（3）若将十字框上下左右移动，可框住另外的五个数，其中五个数的和能等于2018吗？如能，写出这五个数，如不能，说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
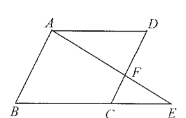
【题目】已知：如图，AD∥BE，∠B=∠D，直线AB与DC平行吗？说明理由（请在下面的解答过程的空格内填空或在括号内填写理由）。
解：直线AB与DC平行.理由如下：
∵ AD∥BE （已知 ）
∴ ∠D = ∠DCE （ ）
又∵∠B = ∠D （ ）
∴∠B = ∠_____ （等量代换）
∴ AB∥DC （ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
问题“已知
且
，
，试确定
的取值范围”有如下解法：
解：
又
又
①
同理得：
②
即
，
请按照上述方法，完成下列问题：
（1）已知关于
、
的方程组
的解均为负数，若
且
，求
的取值范围．
（2）已知
，
，若
成立，求的取值范围（结果用含
的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半．这样的图形有（ ）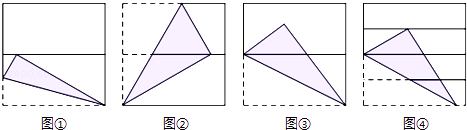
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
