
【题目】已知BE平分∠ABD,DE平分∠BDC,且∠BED =∠ABE +∠EDC.
(1)如图1,求证:AB//CD;
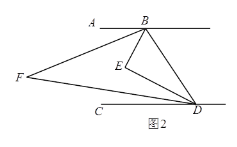
(2)如图2,若∠ABE=3∠ABF,且∠BFD=30°时,试求![]() 的值;
的值;
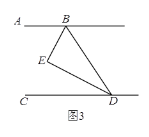
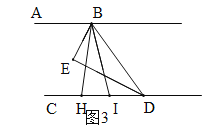
(3)如图3,若H是直线CD上一动点(不与D重合),BI平分∠HBD,画出图形,并探究出∠EBI与∠BHD的数量关系.
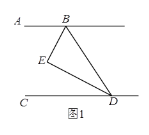
【答案】(1)证明见解析;(2)![]() ;(3)∠BHD=2∠EBI或∠BHD+2∠EBI=180°.
;(3)∠BHD=2∠EBI或∠BHD+2∠EBI=180°.
【解析】
(1)由∠BED =∠ABE +∠EDC和三角形内角和定理即可得到∠ABD+∠BDC=180°,再由同旁内角互补,两直线平行即可得到结论;
(2)由角平分线定义和∠ABD+∠BDC=180°,得到∠BED=∠ABE+∠EDC=90°.
设∠ABF=α,则∠ABE=3α,过F作FG∥AB,则有∠ABF+∠CDF=∠BFD,得到∠CDF=30°-α.过E作EH∥AB,同理可得:∠CDE=90°-3α,根据角的和差得到∠FDE=60°-2α,即可得到结论;
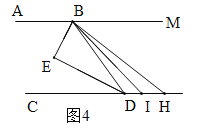
(3)分两种情况讨论:①当H在点D的左边时,②当H在点D右边时.
(1)∵∠BED =∠ABE +∠EDC,∠EBD+∠BED+∠BDE=180°,∴∠ABD+∠BDC=180°,∴AB∥CD;
(2)∵BE平分∠ABD,DE平分∠BDC,∴∠ABE=∠EBD,∠EDC=∠EDB.
∵∠ABD+∠BDC=180°,∴∠BED=∠ABE+∠EDC=90°.
设∠ABF=α,则∠ABE=3α.
过F作FG∥AB,则有:∠ABF+∠CDF=∠BFD,∴∠CDF=30°-α.
过E作EH∥AB,则有:∠ABE+∠CDE=∠BED,∴∠CDE=90°-3α,∴∠FDE=60°-2α,∴![]() .
.
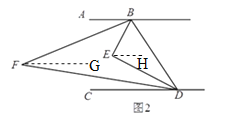
(3)分两种情况讨论:
①当H在点D的左边时,如图3.
设∠HBI=∠DBI=x,∠EBH=y,则∠EBD=2x+y,∴∠ABE=∠EBD=2x+y.
∵AB∥CD,∴∠BHD=∠ABH=2x+y+y=2(x+y)=2∠EBI;
②当H在点D右边时,如图4.
设∠HBI=∠DBI=x,∠EBD=y,则∠EBI=x+y,∴∠ABH=2x+2y.
∵AB∥CD,∴∠ABH+∠BHD=180°,∴2x+2y+∠BHD=180°,∴∠BHD+2∠EBI=180°.
综上所述:∠BHD=2∠EBI或∠BHD+2∠EBI=180° .


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其中部分图象如图所示,下列结论错误的是( )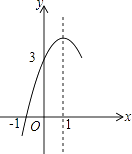
A.4ac<b2
B.方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
C.当y>0时,x的取值范围是﹣1≤x<3
D.当x<0时,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,﹣2),B(6,﹣2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.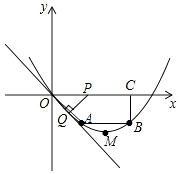
(1)求经过O、A、B三点的抛物线的解析式;
(2)若将△OPQ沿着直线PQ翻折得到△O′PQ,则当t=时,点O′恰好在抛物线上.
(3)在(2)的条件下,记△O′PQ与四边形OABC重叠的面积为S,求S与t的函数关系式,并注明自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 . 
(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣ ![]() ).
).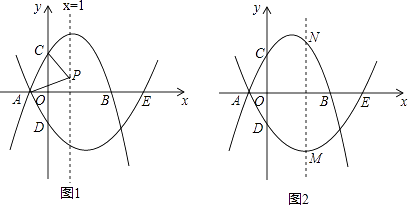
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(x1 , y1),(x2 , y2),(x3 , y3)都是反比例函数y=﹣ ![]() 图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )
A.x1<x2<x3
B.x1<x3<x2
C.x2<x1<x3
D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形![]() 内,若两张边长分别为
内,若两张边长分别为![]() 和
和![]() (
(![]() )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形总未被这两张正方形纸片覆盖的部分用阴影表示,若图1中阴影部分的面积为
)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形总未被这两张正方形纸片覆盖的部分用阴影表示,若图1中阴影部分的面积为![]() ,图2中阴影部分的面积和为
,图2中阴影部分的面积和为![]() ,则关于
,则关于![]() ,
,![]() 的大小关系表述正确的是( )
的大小关系表述正确的是( )
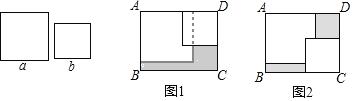
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com