
����Ŀ����֪��������l1��y=��x2+bx+3��x���ڵ�A��B������A�ڵ�B����ࣩ����y���ڵ�C����Գ���Ϊx=1��������l2������A����x�����һ������ΪE��5��0������y���ڵ�D��0���� ![]() ����
����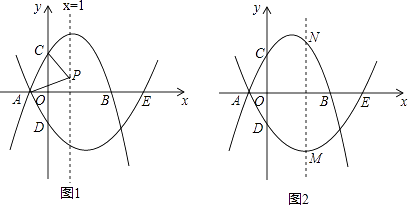
��1����������l2�ĺ�������ʽ��
��2��PΪֱ��x=1��һ���㣬����PA��PC����PA=PCʱ�����P�����ꣻ
��3��MΪ������l2��һ���㣬����M��ֱ��MN��y�ᣬ��������l1�ڵ�N�����M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵ��
���𰸡�
��1���⣺��������l1��y=��x2+bx+3�ĶԳ���Ϊx=1��
�ੁ ![]() =1�����b=2��
=1�����b=2��
��������l1�Ľ���ʽΪy=��x2+2x+3��
��y=0���ɵé�x2+2x+3=0�����x=��1��x=3��
��A����������1��0����
��������l2������A��E���㣬
�����������l2����ʽΪy=a��x+1����x��5����
�֡�������l2��y���ڵ�D��0���� ![]() ����
����
�ੁ ![]() =��5a�����a=
=��5a�����a= ![]() ��
��
��y= ![]() ��x+1����x��5��=
��x+1����x��5��= ![]() x2��2x��
x2��2x�� ![]() ��
��
��������l2�ĺ�������ʽΪy= ![]() x2��2x��
x2��2x�� ![]()
��2���⣺��P������Ϊ��1��y�����ɣ�1���ɵ�C������Ϊ��0��3����
��PC2=12+��y��3��2=y2��6y+10��PA2=[1������1��]2+y2=y2+4��
��PC=PA��
��y2��6y+10=y2+4�����y=1��
��P��������1��1��
��3���⣺���������M��x�� ![]() x2��2x��
x2��2x�� ![]() ����
����
��MN��y�ᣬ
��N��x����x2+2x+3���� ![]() x2��2x��
x2��2x�� ![]()
�x2+2x+3= ![]() x2��2x��
x2��2x�� ![]() ���ɽ��x=��1��x=
���ɽ��x=��1��x= ![]() ��
��
�ٵ���1��x�� ![]() ʱ��MN=����x2+2x+3������
ʱ��MN=����x2+2x+3������ ![]() x2��2x��
x2��2x�� ![]() ��=��
��=�� ![]() x2+4x+
x2+4x+ ![]() =��
=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
��Ȼ��1�� ![]() ��
�� ![]() ���൱x=
���൱x= ![]() ʱ��MN�����ֵ
ʱ��MN�����ֵ ![]() ��
��
�ڵ� ![]() ��x��5ʱ��MN=��
��x��5ʱ��MN=�� ![]() x2��2x��
x2��2x�� ![]() ��������x2+2x+3��=
��������x2+2x+3��= ![]() x2��4x��
x2��4x�� ![]() =
= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��Ȼ��x�� ![]() ʱ��MN��x�����������
ʱ��MN��x�����������
�൱x=5ʱ��MN�����ֵ�� ![]() ����5��
����5�� ![]() ��2��
��2�� ![]() =12��
=12��
���Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12
����������1����������l1�ĶԳ���Ϊx=1���õ�b=2���õ�������l1�Ľ���ʽ���õ�A������Ϊ����1��0�����ɴ���ϵ�������������l2 �ĺ�������ʽ����2�����P�����꣬�ɣ�1���ɵ�C�����꣬��PC=PA���õ�P������Ϊ��1��1������3������������M������꣬��MN��y�ᣬ�õ�N�����꣬�ó�MN�����ֵ ![]() ���ڵ�
���ڵ� ![]() ��x��5ʱ ����Ȼ��x��
��x��5ʱ ����Ȼ��x�� ![]() ʱ��MN��x��������������Ե�x=5ʱ��MN�����ֵ�����Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12���������ۺ��⣬�ѶȽϴ���ͽⷽ��ʱ��������ϸ.
ʱ��MN��x��������������Ե�x=5ʱ��MN�����ֵ�����Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12���������ۺ��⣬�ѶȽϴ���ͽⷽ��ʱ��������ϸ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1����һ����Ϊ 2m����Ϊ 2n �ij����Σ���ͼ�������ü���������ֳ��ĸ���ȫ��ͬ��С�����Σ�Ȼ��ͼ 2 ����״ƴͼ��
(1)ͼ 2 �е�ͼ����Ӱ���ֵı߳�Ϊ ��(�ú� m��n �Ĵ���ʽ��ʾ)
(2)���������ֲ�ͬ�ķ����ֱ���ͼ 2 ����Ӱ���ֵ������ ����һ�� ���������� ��
(3)�۲�ͼ 2����д������ʽ(m+n)2��(m��n)2��4mn ֮��Ĺ�ϵʽ�� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ1��ͼ2��������״����С��ȫ��ͬ�����������е�ÿ��С�����εı߳���Ϊ![]() �����и���һ����ȫ��ͬ�������Σ�����ͼ1��ͼ2�ֱ���һ��ֱ�ߣ���������Ҫ��
�����и���һ����ȫ��ͬ�������Σ�����ͼ1��ͼ2�ֱ���һ��ֱ�ߣ���������Ҫ��

��1��ֱ���������εĽ���Ҫ��������ĸ�㣨ÿ��С�����εĶ����Ϊ��㣩
��2����ͼ1��ͼ2�зֱ��ò�ͬ�ķ����������ηֳ�����ͼ������һ������������һ�����ı��Σ��ָ��������ε������Ϊ![]() ���ı��ε����Ϊ
���ı��ε����Ϊ![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��
��1����֤��OE=OF��
��2����CE=12��CF=5����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
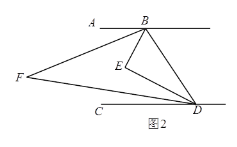
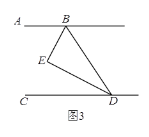
����Ŀ����֪BEƽ����ABD��DEƽ����BDC������BED =��ABE +��EDC��
��1����ͼ1����֤��AB//CD��
��2����ͼ2������ABE=3��ABF������BFD=30��ʱ������![]() ��ֵ��
��ֵ��
��3����ͼ3����H��ֱ��CD��һ���㣨����D�غϣ���BIƽ����HBD������ͼ�Σ���̽������EBI����BHD��������ϵ��
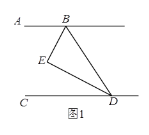
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һЩ��ȫ��ͬ��С�������ɵļ����������ͼ������ͼ���������������С������ĸ��������ǣ� ��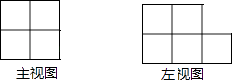
A.5��
B.6��
C.7��
D.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Աij��Ĺ��������ͼ��ʾ�����е�![]() ��
��![]() ��
��![]() �ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ�������
�ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ�������![]() ��
��![]() ��
��![]() ���ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ���.�������������ۣ����������Ϳ������ʱ����̵��Ǽף����������Ϳ�ݼ��������DZ���������һ�������Ϳ���ܼ�����������.���������У�������ȷ���۵�����ǣ� ��
���ĺᡢ������ֱ��ʾ�ס��ҡ����������Ա�������Ϳ�����õ�ʱ��ͼ���.�������������ۣ����������Ϳ������ʱ����̵��Ǽף����������Ϳ�ݼ��������DZ���������һ�������Ϳ���ܼ�����������.���������У�������ȷ���۵�����ǣ� ��
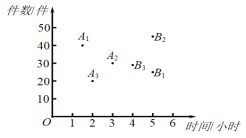
A. �٢�B. �٢�C. ��D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=1����P��BC���ϵ�����һ�㣨���ڶ˵�B��C��������AP����B��D������BE��AP�ڵ�E��DF��AP�ڵ�F.
��1����֤��EF=DF��BE��
��2������ADF���ܳ�Ϊ![]() ����EF�ij�.
����EF�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ǹ������Խ��ͬѧ���ڷ��ֽ̲��е��÷������������ƶ��Ĺ��ɺ�ͻ�����룬��������ż��2��4��6��8�����ų����±�,����һ��ʮ���ο��ס���е������,������ϸ�۲�ʮ���ο�������ֵĹ���,���ش���������:
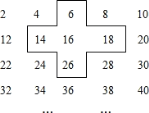
![]() ʮ�ֿ��е�������ĺ����м����16��ʲô��ϵ?
ʮ�ֿ��е�������ĺ����м����16��ʲô��ϵ?
![]() ���м����Ϊx���ô���ʽ��ʾʮ�ֿ��е�������ĺͣ�
���м����Ϊx���ô���ʽ��ʾʮ�ֿ��е�������ĺͣ�
��3������ʮ�ֿ����������ƶ����ɿ�ס����������������������ĺ��ܵ���2018�����ܣ�д������������粻�ܣ�˵�����ɡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com