
【题目】在平面直角坐标系xOy中,点P,Q(两点可以重合)在x轴上,点P的横坐标为m,点Q的横坐标为n,若平面内的点M的坐标为(n,|m﹣n|),则称点M为P,Q的跟随点.
(1)若m=0,
①当n=3时,P,Q的跟随点的坐标为 ;
②写出P,Q的跟随点的坐标;(用含n的式子表示);
③记函数y=kx﹣1(﹣1≤x≤1,k≠0)的图象为图形G,若图形G上不存在P,Q的跟随点,求k的取值范围;
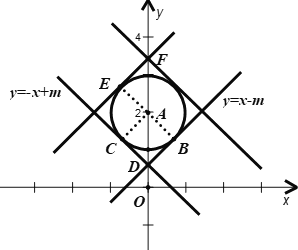
(2)⊙A的圆心为A(0,2),半径为1,若⊙A上存在P,Q的跟随点,直接写出m的取值范围.
【答案】(1)①(3,3);②(n,n)或(n,﹣n);③﹣2<k<0或0<k<2;(2)﹣2![]() m
m![]() 2或2
2或2![]() m≤2
m≤2![]()
【解析】
(1)①将m和n的值代入点M的坐标表达式中计算即可;
②将![]() 代入点M的坐标表达式,再分
代入点M的坐标表达式,再分![]() 和
和![]() 两种情况,去绝对值即可得;
两种情况,去绝对值即可得;
③根据②得出点M所在的函数图象,再画出图象,分![]() 和
和![]() 两种情况讨论,分别建立不等式求解即可;
两种情况讨论,分别建立不等式求解即可;
(2)先由跟随点的定义得出点M在![]() 的图象上,再根据直线与圆的位置关系确认符合题意的临界值,然后利用三角函数值、线段的距离求解即可.
的图象上,再根据直线与圆的位置关系确认符合题意的临界值,然后利用三角函数值、线段的距离求解即可.
(1)①把![]() 代入点P,Q的跟随点M的坐标
代入点P,Q的跟随点M的坐标![]()
故答案为:![]() ;
;
②把![]() 代入P,Q的跟随点M的坐标
代入P,Q的跟随点M的坐标![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以P,Q的跟随点的坐标为![]() 或
或![]() ;
;
③由②可知,当![]() 时,P,Q的跟随点在函数
时,P,Q的跟随点在函数![]() 或
或![]() 的图象上
的图象上
由题意,需分![]() 和
和![]() 两种情况:
两种情况:
当![]() 时,如图,要使图形G上不存在P,Q的跟随点,则在
时,如图,要使图形G上不存在P,Q的跟随点,则在![]() 处,
处,![]() 的函数值需小于
的函数值需小于![]() 的函数值,即
的函数值,即![]() ,解得
,解得![]()
故此时k的取值范围为![]()
当![]() 时,如图,要使图形G上不存在P,Q的跟随点,则在
时,如图,要使图形G上不存在P,Q的跟随点,则在![]() 处,
处,![]() 的函数值需小于
的函数值需小于![]() 的函数值,即
的函数值,即![]() ,解得
,解得![]()
故此时k的取值范围为![]()
综上,k的取值范围为![]() 或
或![]() ;
;
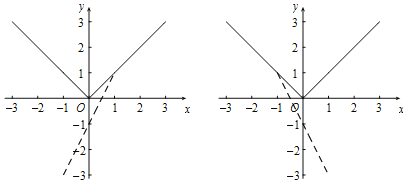
(2)由跟随点的定义可知,点M在![]() 的图象上,即点M在
的图象上,即点M在![]() 或
或![]() 的图象上
的图象上
如图,当直线与圆A相切时,是符合要求的临界位置
当点M在![]() 的图象上时,直线与y轴的交点坐标为
的图象上时,直线与y轴的交点坐标为![]()
由直线的解析式和圆的切线性质得:![]()
则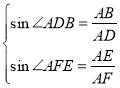 ,即
,即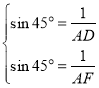 ,解得
,解得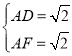
![]() 点A坐标为
点A坐标为![]()
![]() ,解得
,解得![]()
![]() ,解得
,解得![]()
故此时m的取值范围为![]()
同理可得:当点M在![]() 图象上时,m的取值范围为
图象上时,m的取值范围为![]()
综上,m的取值范围为![]() 或
或![]() .
.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
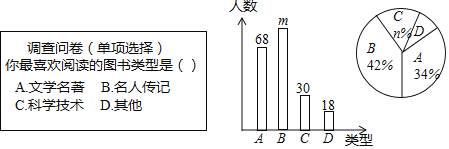
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0),与y轴交于C(0,-3)

(1)求抛物线C1的表达式;
(2)分别写出抛物线C1关于B点,关于A点的对称抛物线C2, C3的函数表达式
(3)设C1的顶点为D,C2与x轴的另一个交点为A1顶点为D1,C3与x轴的另一个交点为B1,顶点为D2,在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中,求面积最大的四边形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂接到一批订单,按要求要20天内完成,每件产品的出厂价为40元,每件产品的生产成本m元与时间x天(x为整数)之间的一次函数关系如下表:
天数(x) | 1 | 4 | 6 | … |
每件成本(m) | 23 | 20 | 18 | … |
小张每天生产的件数y件与x天(x为整数)之间满足如下关系为:![]() .
.
(1)求m与x之间的函数关系式;
(2)若第x天的利润为W元,求W与x之间的函数关系式,并求出小张在哪天利润最大,最大利润是多少元;
(3)在生产的前10天中,公司决定每件产品捐赠a元(a<7)给公益事业,调查发现,扣除捐赠后的日销售利润随x增大而增大,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
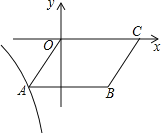
【题目】如图,在平面直角坐标系xOy中,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,函数y![]() (x<0)的图象经过点A.
(x<0)的图象经过点A.
(1)求k的值;
(2)若过点A的直线l平行于直线OB,且交函数y![]() (x<0)的图象于点D.
(x<0)的图象于点D.
①求直线l的表达式;
②定义:横、纵坐标都是整数的点叫做整点.记函数y![]() (x<0)的图象在点A,D之间的部分与线段AD围成的区域(含边界)为W.结合函数图象,直接写出区域W内(含边界)的整点个数.
(x<0)的图象在点A,D之间的部分与线段AD围成的区域(含边界)为W.结合函数图象,直接写出区域W内(含边界)的整点个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
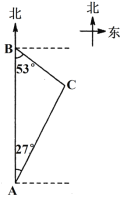
【题目】如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈![]() ,cos27°≈
,cos27°≈![]() ,tan27°≈
,tan27°≈![]() ,sin53°≈
,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的布袋中装有1个红球,2个白球,它们除颜色外其余完全相同.
(1)从袋中任意摸出两个球,试用树状图或表格列出所有等可能的结果,并求摸出的球恰好是两个白球的概率;
(2)若在布袋中再添加a个白球,充分搅匀,从中摸出一个球,使摸到红球的概率为![]() ,试求a的值.
,试求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com