
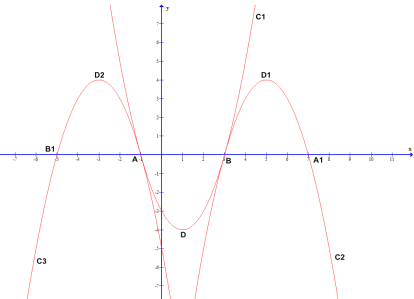
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0),与y轴交于C(0,-3)

(1)求抛物线C1的表达式;
(2)分别写出抛物线C1关于B点,关于A点的对称抛物线C2, C3的函数表达式
(3)设C1的顶点为D,C2与x轴的另一个交点为A1顶点为D1,C3与x轴的另一个交点为B1,顶点为D2,在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中,求面积最大的四边形的面积。
【答案】(1)抛物线C1的表达式为:y=x-2x-3;(2)抛物线C2表达式为:y2=-x2+10x-21;抛物线C3表达式为:y3= -x2-6x-5;(3)48.
【解析】
(1)将点B(3,0),C(0,-3)代入y=x+bx+c求出b,c即可得到抛物线C1的表达式;
(2)求出A点坐标,可得AB=4,根据关于点成中心对称的图形的性质,可求出抛物线C2, C3的函数表达式;
(3)求出A、B、D、A1、B1、D1、D2这七个点的坐标,根据图形,计算几个面积较大的四边的面积,比较即可得到面积最大的四边形的面积.
解:(1)将点B(3,0),C(0,-3)代入y=x+bx+c可得:![]() ,
,
解得:![]() ,
,
∴抛物线C1的表达式为:y=x-2x-3;
(2)令y=x-2x-3=0,解得:x1=3,x2=-1,
∴A(-1,0),
∴AB=4,
∴抛物线C2过点(3,0)和点(7,0)
设抛物线C2解析式为:y2=a(x-3)(x-7),
∵抛物线C2与抛物线C1关于B点对称,
∴a=-1,即抛物线C2解析式为:y2=-(x-3)(x-7)=-x2+10x-21,
同理可得:抛物线C3解析式为:y3=-(x+5)(x+1)= -x2-6x-5;
(3)如图,由题意得:A(-1,0),B(3,0),A1(7,0),B1(-5,0),
∵抛物线C1:y=x-2x-3=(x-1)2-4,
∴D(1,-4),
同理:D1(5,4),D2(-3,4),
∴S梯形B1 D2 D1 A1=![]() ,
,
S四边形B1D2DD1 = S四边形A1D1D2D =S平行四边形B1D2D1B+S△B1DB=![]() ,
,
S四边形B1DA1D1 = S四边形A1DB1D2 =S△B1DA1+ S△B1A1D1=![]() ,
,
(注:面积明显较小的四边形面积不予计算)
综上所述,面积最大的四边形的面积是48.


科目:初中数学 来源: 题型:
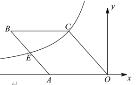
【题目】如图,在平面直角坐标系中,菱形 ABCO 的一边 OA 在 x 轴上,![]() ,反比例函数
,反比例函数![]() 过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=9,点C为线段AB上一点,AC=3,点D为平面内一动点,且满足CD=3,连接BD将BD绕点D逆时针旋转90到DE,连接BE、AE,则AE的最大值为 ________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
![]() 若去丙地的车票占全部车票的
若去丙地的车票占全部车票的![]() ,则总票数为______ 张,去丁地的车票有______ 张
,则总票数为______ 张,去丁地的车票有______ 张![]()
![]() 若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张
若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张![]() 所有车票的形状、大小、质地完全相同、均匀
所有车票的形状、大小、质地完全相同、均匀![]() ,那么员工小胡抽到去甲地的车票的概率是多少?
,那么员工小胡抽到去甲地的车票的概率是多少?
![]() 若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李
若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李![]() 请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.
请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.

查看答案和解析>>
科目:初中数学 来源: 题型:
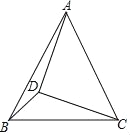
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P,Q(两点可以重合)在x轴上,点P的横坐标为m,点Q的横坐标为n,若平面内的点M的坐标为(n,|m﹣n|),则称点M为P,Q的跟随点.
(1)若m=0,
①当n=3时,P,Q的跟随点的坐标为 ;
②写出P,Q的跟随点的坐标;(用含n的式子表示);
③记函数y=kx﹣1(﹣1≤x≤1,k≠0)的图象为图形G,若图形G上不存在P,Q的跟随点,求k的取值范围;
(2)⊙A的圆心为A(0,2),半径为1,若⊙A上存在P,Q的跟随点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市政府大力扶持大学生创业,童威在政府的扶持下投资销售一种进价为每盏20元的护眼台灯,销售过程中发现,每月销售量y(盏)与销售单价x(元)之间的关系可近似地看作一次函数:y=﹣10x+500.
(1)设每月获得的利润为w(元),求w与x的关系式.
(2)如果想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元.如果童威想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com