
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.
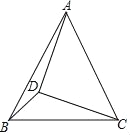
【答案】5![]()
【解析】
作辅助线,构建全等三角形和高线DH,设CM=a,根据等腰直角三角形的性质和三角函数表示AC和AM的长,根据三角形面积表示DH的长,证明△ADG≌△CDH(AAS),可得DG=DH=MG=作辅助线,构建全等三角形和高线DH,设CM=a,根据等腰直角三角形的性质和三角函数表示AC和AM的长,根据三角形面积表示DH的长,证明△ADG≌△CDH(AAS),可得DG=DH=MG=![]() ,AG=CH=a+
,AG=CH=a+![]() ,根据AM=AG+MG,列方程可得结论.,AG=CH=a+
,根据AM=AG+MG,列方程可得结论.,AG=CH=a+![]() ,根据AM=AG+MG,列方程可得结论.
,根据AM=AG+MG,列方程可得结论.
过D作DH⊥BC于H,过A作AM⊥BC于M,过D作DG⊥AM于G,
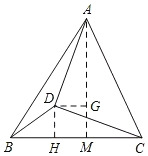
设CM=a,
∵AB=AC,
∴BC=2CM=2a,
∵tan∠ACB=2,
∴![]() =2,
=2,
∴AM=2a,
由勾股定理得:AC=![]() a,
a,
S△BDC=![]() BCDH=10,
BCDH=10,
![]() 2aDH=10,
2aDH=10,
DH=![]() ,
,
∵∠DHM=∠HMG=∠MGD=90°,
∴四边形DHMG为矩形,
∴∠HDG=90°=∠HDC+∠CDG,DG=HM,DH=MG,
∵∠ADC=90°=∠ADG+∠CDG,
∴∠ADG=∠CDH,
在△ADG和△CDH中,
∵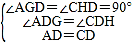 ,
,
∴△ADG≌△CDH(AAS),
∴DG=DH=MG=![]() ,AG=CH=a+
,AG=CH=a+![]() ,
,
∴AM=AG+MG,
即2a=a+![]() +
+![]() ,
,
a2=20,
在Rt△ADC中,AD2+CD2=AC2,
∵AD=CD,
∴2AD2=5a2=100,
∴AD=5![]() 或5
或5![]() (舍),
(舍),
故答案为:5![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).
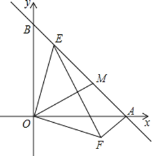
(1)求线段AB的长;
(2)若点E在线段AB上,OE⊥OF,且OE=OF,求AE+AF的值;
(3)在(2)的条件下,过O作OM⊥EF,交AB于M,试确定线段BE、EM、AM之间的数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
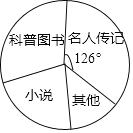
【题目】2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动,200多所学校的师生踊跃参与,向新疆疏勒县中小学共捐赠爱心图书28.5万余本.某学校学生社团对本校九年级学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
图书种类 | 频数(本) | 频率 |
名人传记 | 175 | a |
科普图书 | b | 0.30 |
小说 | 110 | c |
其他 | 65 | d |
(1)求该校九年级共捐书多少本;
(2)统计表中的a= ,b= ,c= ,d= ;
(3)若该校共捐书1500本,请估计“科普图书”和“小说”一共多少本;
(4)该社团3名成员各捐书1本,分别是1本“名人传记”,1本“科普图书”,1本“小说”,要从这3人中任选2人为受赠者写一份自己所捐图书的简介,请用列表法或树状图求选出的2人恰好1人捐“名人传记”,1人捐“科普图书”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
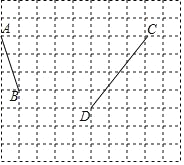
【题目】如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以AB为斜边的等腰直角三角形ABE,点E在小正方形的顶点上;
(2)在方格纸中画出以CD为对角线的矩形CMDN(顶点字母按逆时针顺序),且面积为10,点M、N均在小正方形的顶点上;
(3)连接ME,并直接写出EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,直角边为a、b,斜边为c.若把关于x的方程ax2+![]() cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 一定有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 点
点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
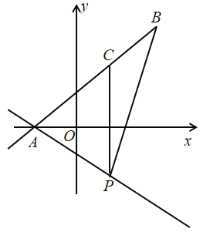
(1)![]() 的值为 ;
的值为 ;
(2)用含有![]() 的式子表示线段
的式子表示线段![]() 的长;
的长;
(3)若![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数表达式,并求出当
之间的函数表达式,并求出当![]() 最大时点
最大时点![]() 的坐标;
的坐标;
(4)在(3)的条件下,把直线![]() 沿着
沿着![]() 轴向下平移,交
轴向下平移,交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,在平移的过程中,当
,在平移的过程中,当![]() 时,请直接写出点
时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com