
【题目】在Rt△ABC中,直角边为a、b,斜边为c.若把关于x的方程ax2+![]() cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 一定有实数根
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,为迎接第
个世界读书日,为迎接第![]() 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按![]() 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.


第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
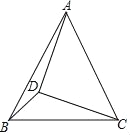
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,对角线AC与BD相交于点O,经过点O的直线与边AB相交于点E,与边CD相交于点F.

(1)求证:OE=OF;
(2)如图2,连接DE,BF,当DE⊥AB时,在不添加其他辅助线的情况下,直接写出腰长等于![]() BD的所有的等腰三角形.
BD的所有的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设![]() (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为
(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为![]() 千米,骑自行车学生骑行的路程为
千米,骑自行车学生骑行的路程为![]() 千米,
千米,![]() 关于
关于![]() 的函数图象如图所示.
的函数图象如图所示.
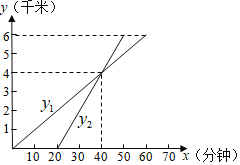
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
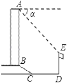
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,则大楼AB的高度为________米.
,则大楼AB的高度为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
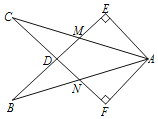
【题目】如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com