
【题目】问题原型:如图①,正方形ABCD的对角线交于点O,点E、F分别为边AB、AD中点,且∠EOF=90°,易得四边形AEOF的面积是正方形ABCD的面积的四分之一.(不用证明)
探究发现:某数学兴趣小组,尝试改变点E、F的位置,点E、F分别为边AB、AD上任一点,且∠EOF=90°,如图②,探究:四边形AEOF的面积是否为正方形ABCD面积的四分之一?并说明理由.
拓展提升:如图③,菱形ABCD中,∠BAD=120°,∠EAF=60°,且点E、F分别在边DC、BC上,四边形AECF的面积是菱形ABCD面积的几分之一?(直接写出结果即可)
【答案】解:探究发现,四边形AEOF的面积是否为正方形ABCD面积的四分之一.
理由:如图②中,
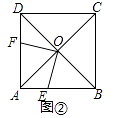
∵四边形ABCD是正方形,
∴DO=AO,∠ODF=∠OAE=45°,∠DOA=90°,△AOD的面积是正方形ABCD面积的四分之一,
∵∠EOF=90°,
∴∠AOE+∠AOF=90°,又∠ODF=∠AOF=∠DOA=90°,
∴∠AOE=∠DOF,
∴△AOE≌△DOF,
∴S四边形AEOF=S△AOD,
∴S四边形AEOF= ![]() S正方形ABCD.
S正方形ABCD.
拓展提升:结论:S四边形AEGF= ![]() S菱形ABGD.
S菱形ABGD.
理由:如图③中,连接AG.
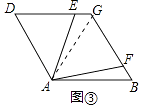
∵四边形ABGD是菱形,∠DAB=120°,
∴AB=BG=GD=AD,∠GAD=∠GAB=60°,
∴△ADG和△ABG都是等边三角形,
∴∠D=∠AGF=60°,AD=AG,
∵∠DAG=∠EAF=60°,
∴∠DAE=∠GAF,
∴△DAE≌△GAF,
∴S△DAE=S△GAF,
∴S四边形AEGF=S△ADG= ![]() S菱形ABGD.
S菱形ABGD.
【解析】探究发现:只要证明△AOE≌△DOF,可得S四边形AEOF=S△AOD,推出S四边形AEOF= ![]() S正方形ABCD;
S正方形ABCD;
拓展提升:结论:S四边形AEGF= ![]() S菱形ABGD.只要证明△DAE≌△GAF即可解决问题;
S菱形ABGD.只要证明△DAE≌△GAF即可解决问题;


科目:初中数学 来源: 题型:
【题目】如图,我国![]() 年税收收入及其增长速度的不完整统计图
年税收收入及其增长速度的不完整统计图![]() 请你根据图中已有信息,解答下列问题:
请你根据图中已有信息,解答下列问题:

![]() 这5年中,哪一年至哪一年的年税收收入增长率持续上升?
这5年中,哪一年至哪一年的年税收收入增长率持续上升?
![]() 求出2008年我国的年税收收入
求出2008年我国的年税收收入![]() 精确到1亿元
精确到1亿元![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )

A. 115° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面内有四个点,它们的坐标分别是A(-1,0),B(2+![]() ,0),C(2,1),D(0,1).
,0),C(2,1),D(0,1).
(1)依次连接A,B,C,D围成的四边形是一个_____________形;
(2)求这个四边形的面积;
(3)将这个四边形向左平移![]() 个单位长度,四个顶点的坐标分别为多少?
个单位长度,四个顶点的坐标分别为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是 ( )
x | 6.17 | 6.18 | 6.19 | 6.20 |
y=ax2+bx+c | 0.02 | 0.01 | 0.02 | 0.04 |
A.0B.1C.2D.1或2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com