
 如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是$\frac{15\sqrt{3}}{4}$-$\frac{3}{2}$π.
如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是$\frac{15\sqrt{3}}{4}$-$\frac{3}{2}$π. 分析 连接连接OD、CD,根据S阴=S△ABC-S△ACD-(S扇形OCD-S△OCD)计算即可解决问题.
解答 解:如图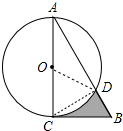 ,连接OD、CD.
,连接OD、CD.
∵AC是直径,
∴∠ADC=90°,
∵∠A=30°,
∴∠ACD=90°-∠A=60°,
∵OC=OD,
∴△OCD是等边三角形,
∵BC是切线.
∴∠ACB=90°,∵BC=2$\sqrt{3}$,
∴AB=4$\sqrt{3}$,AC=6,
∴S阴=S△ABC-S△ACD-(S扇形OCD-S△OCD)
=$\frac{1}{2}$×6×2$\sqrt{3}$-$\frac{1}{2}$×3×3$\sqrt{3}$-($\frac{60π×{3}^{2}}{360}$-$\frac{\sqrt{3}}{4}$×32)
=$\frac{15\sqrt{3}}{4}$-$\frac{3}{2}$π.
故答案为:$\frac{15\sqrt{3}}{4}$-$\frac{3}{2}$π.
点评 本题考查扇形面积公式、直角三角形30度角性质、等边三角形性质等知识,解题的关键是学会分割法求面积,属于中考常考题型.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).
在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
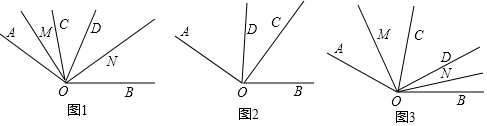
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com