
【题目】如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线![]() 恰好经过边AB的四等分点E(BE<AE),则k的值为____________.
恰好经过边AB的四等分点E(BE<AE),则k的值为____________.

【答案】-![]()
【解析】
由AD∥BC,可得出S△BCD=S△BCA、S△ACD=S△ABD,根据△ACD与△BCD的面积分别为10和20结合同底三角形面积的性质,即可得出AO:OC=DO:OB=1:2,进而可得出S△AOB=![]() ,再根据反比例函数系数k的几何意义以及相似三角形的性质得出|k|=
,再根据反比例函数系数k的几何意义以及相似三角形的性质得出|k|=![]() ,解之即可得出结论.
,解之即可得出结论.
∵AD∥BC,
∴S△BCD=S△BCA,S△ACD=S△ABD.
∵△ACD与△BCD的面积分别为10和20,
∴△ABD和△BCD面积比为1:2,
∴根据同底得:AO:OC=DO:OB=1:2,
∴S△AOB=![]() .
.
∵双曲线![]() 恰好经过边AB的四等分点E(BE<AE),
恰好经过边AB的四等分点E(BE<AE),
∴![]() S△AOB+|k|+
S△AOB+|k|+![]() S△AOB=S△AOB,
S△AOB=S△AOB,
∴|k|=![]() S△AOB=
S△AOB=![]() ,
,
∵双曲线经过第二象限,k<0,
∴k=-![]() .
.
故答案为-![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若一个三位数两个数位上数字的和等于另一个数位上的数字,则称这个三位数为“均衡三位数”.现从1,2,3,4,5这5个数字中任取三个数字,组成无重复数字且百位数字、十位数字、个位数字依次增大的三位数.
(1)请列举出所有可能得到的三位数;
(2)小明和小亮玩一个游戏,游戏规则如下:若(1)中组成的三位数是“均衡三位数”,则小明胜;否则小亮胜.这个游戏公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,
,![]() 点坐标为
点坐标为![]() ,将直线
,将直线![]() 在
在![]() 轴下方的部分记作
轴下方的部分记作![]() ,作
,作![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() .
.
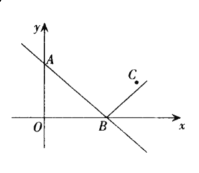
(1)求![]() 的坐标;
的坐标;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 经过点
经过点![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___________ (结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
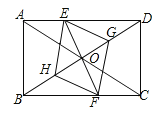
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°,且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积.(结果精确到0.01)
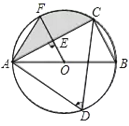
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别为△ABC的边AB、AC上的点,BE与CD相交于点O,现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD,选择其中2个条件作为题设,余下2个条件作为结论,所有命题中,真命题的个数为( )
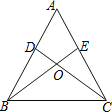
A. .3B. .4C. .5D. 、6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边AB的中点,点F是边CD上一点,连接ED,EF,ED平分∠AEF,过点D作DG⊥EF于点M,交BC于点G,连接GE,GF,若FG∥DE,则![]() 的值是( )
的值是( )
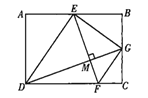
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com