

| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
|
|
|
|
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:
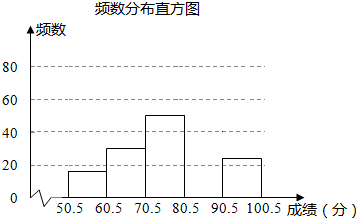
| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5~60.5 | 16 | 0.08 |
| 二 | 60.5~70.5 | 30 | 0.15 |
| 三 | 70.5~80.5 | 50 | 0.25 |
| 四 | 80.5~90.5 | m | 0.40 |
| 五 | 90.5~100.5 | 24 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com