
| A. | 20厘米 | B. | 19.5厘米 | C. | 14.5厘米 | D. | 10厘米 |
分析 根据题意,把实际问题抽象成几何问题,即圆中与弦有关的问题,根据垂径定理,构造直角三角形,小坑的直径就是圆中的弦长,小坑的深就是拱高,利用勾股定理,设出未知数,列出方程,即可求出铅球的直径.
解答 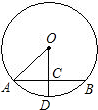 解:根据题意,画出图形如图所示,
解:根据题意,画出图形如图所示,
由题意知,AB=10厘米,CD=2厘米,OD是半径,且OC⊥AB,
∴AC=CB=5厘米,
设铅球的半径为r,则OC=r-2,
在Rt△AOC中,根据勾股定理,OC2+AC2=OA2,
即(r-2)2+52=r2,
解得:r=7.25,
所以铅球的直径为:2×7.25=14.5(厘米).
故选:C.
点评 本题考查了垂径定理的应用和勾股定理.解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+($\frac{a}{2}$)2成立,知道这三个量中的任意两个,就可以求出另外一个.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\sqrt{2}$=2$\sqrt{2}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{27}$÷$\sqrt{3}$=3 | D. | $\sqrt{4}$=±2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
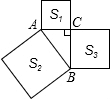 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积.若S1=81,S2=225,则S3=144.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积.若S1=81,S2=225,则S3=144.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
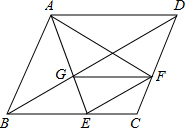 如图,在?ABCD中,点E、F分别在BC、CD上,BE=DF,∠BAF=∠DAE.
如图,在?ABCD中,点E、F分别在BC、CD上,BE=DF,∠BAF=∠DAE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com