
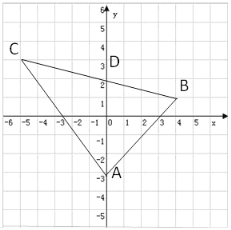
【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
科目:初中数学 来源: 题型:
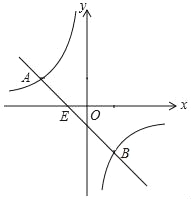
【题目】如图,已知A(﹣4,n),B(4﹣n,﹣4)是直线y=kx+b和双曲线y=![]() 的两个交点.
的两个交点.
(1)求两个函数的表达式;
(2)观察图象,直接写出不等式kx+b﹣![]() ≥0的解集.
≥0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知直线m平行于直线n,折线ABC是夹在m与n之间的一条折线,则![]() 、
、![]() 、
、![]() 的度数之间有什么关系?为什么?
的度数之间有什么关系?为什么?

(2)如图,直线m依然平行于直线n,则此时![]() 、
、![]() 、
、![]() 、
、![]() 之间有什么关系?(只需写出结果)
之间有什么关系?(只需写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=4,AD=BC=6,点A的坐标为(3,2).动点P的运动速度为每秒a个单位长度,动点Q的运动速度为每秒b个单位长度,且![]() .设运动时间为t,动点P、Q相遇则停止运动.
.设运动时间为t,动点P、Q相遇则停止运动.
(1) 求a,b的值;
(2) 动点P,Q同时从点A出发,点P沿长方形ABCD的边界逆时针方向运动,点Q沿长方形ABCD的边界顺时针方向运动,当t为何值时P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
(3) 动点P从点A出发,同时动点Q从点D出发:
①若点P、Q均沿长方形ABCD的边界顺时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
②若点P、Q均沿长方形ABCD的边界逆时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.
(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为 , 设正方形的边长为a,则a= .
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如 ![]() =
= ![]() =
= ![]() .类比此,可以将(1)中的a表示成a= .
.类比此,可以将(1)中的a表示成a= .
(3)![]() =
= ![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为 ![]() ;类比此,(2)中的a可以理解为以长度和为直角边的直角三角形斜边的长.
;类比此,(2)中的a可以理解为以长度和为直角边的直角三角形斜边的长.
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成A、B、C、D、E五部分.
(5)拼一拼:把图②中五部分拼接得到如图③的正方形.
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(1)△CDF与△DEA是否相似?说明理由;
(2)求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com