
【题目】如图,在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=4,AD=BC=6,点A的坐标为(3,2).动点P的运动速度为每秒a个单位长度,动点Q的运动速度为每秒b个单位长度,且![]() .设运动时间为t,动点P、Q相遇则停止运动.
.设运动时间为t,动点P、Q相遇则停止运动.
(1) 求a,b的值;
(2) 动点P,Q同时从点A出发,点P沿长方形ABCD的边界逆时针方向运动,点Q沿长方形ABCD的边界顺时针方向运动,当t为何值时P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
(3) 动点P从点A出发,同时动点Q从点D出发:
①若点P、Q均沿长方形ABCD的边界顺时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
②若点P、Q均沿长方形ABCD的边界逆时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标.

【答案】(1)a=1,b=2;(2) ![]() ,P、Q两点相遇,P,Q两点的坐标为
,P、Q两点相遇,P,Q两点的坐标为![]() ;(3)① t=6,P、Q(1,-2 ),② t=14,P、Q(1,-2 )
;(3)① t=6,P、Q(1,-2 ),② t=14,P、Q(1,-2 )
【解析】
(1)由![]() ,可得
,可得![]() ,
,![]() ,从而可求出a,b的值;
,从而可求出a,b的值;
(2)由相遇可得t+2t=(6+4)×2,求出t的值,进而求出相遇时P、Q所在位置的坐标;
(3)①由相遇可得方程2t-t=6 ,求出t的值,进而求出相遇时P、Q所在位置的坐标;
②由相遇可得方程2t-t=14 ,求出t的值,进而求出相遇时P、Q所在位置的坐标;
(1) ∵![]() ,
,
∴![]() ,
,![]() ,
,
∴a=1,b=2;
(2) ∵t+2t=(6+4)×2,
∴![]() 时,P、Q两点相遇 .
时,P、Q两点相遇 .
![]() -6=
-6=![]() ,2-
,2-![]() =
=![]() ,
,
∴此时P,Q两点相遇时的坐标为![]() ;
;
(3) ① 2t-t=6 , ∴t=6 ,
6-4=2,3-2=1,
∴P、Q两点相遇时的坐标为(1,-2 );
② 2t-t=14 , ∴t=14,
14-6-4=4,4-3=1,
∴P、Q两点相遇时的坐标为(1,-2 ).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两名工人参加操作技能培训.他们在培训期间参加的8次测试成绩记录如下表:
甲 | 73 | 82 | 70 | 85 | 80 | 70 | 75 | 65 |
乙 | 85 | 72 | 78 | 71 | 83 | 69 | 74 | 68 |
则下列说法错误的是( )
A.甲、乙的平均成绩都是75
B.甲成绩的众数是70
C.乙成绩的中位数是73
D.若从中选派一人参加操作技能比赛,从成绩稳定性考虑,应选甲
查看答案和解析>>
科目:初中数学 来源: 题型:
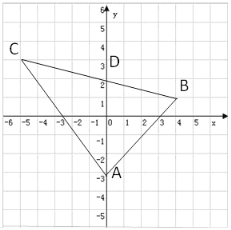
【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
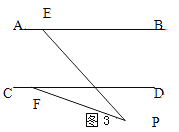
【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
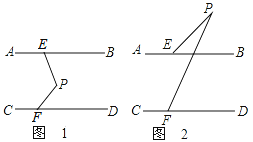
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截.红方行驶26千米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西37°方向前进,刚好在D处成功拦截蓝方.求拦截点D处到公路的距离AD.
(参考数据:sin67°≈ ![]() ,cos67°≈
,cos67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() ,sin37°≈
,sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在△ABC中,∠C=60°,∠A=40°.

(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com